3. Измерение широты и наклона эклиптики
С помощью довольно простых приспособлений широту места можно определить одним из двух методов, известных греческим астрономам еще в -400 г. или даже раньше.
Суть первого метода состоит в следующем. Предположим сначала, что Полярная звезда находится строго над Северным полюсом. Тогда для одного и того же наблюдателя она всегда будет появляться в одном и том же положении. Если наблюдатель находится на экваторе, то Полярная звезда будет на горизонте и ее высота равна нулю. Если наблюдатель переместится на север, то Полярная звезда поднимется над горизонтом и ее высота будет равна широте, на которой находится наблюдатель. То, что Полярная звезда расположена не точно над полюсом, лишь немного усложняет дело. Наблюдатель измеряет наибольшую и наименьшую высоты Полярной звезды и получает широту данного места, взяв среднее арифметическое этих двух величин [1]).
Другой метод, видимо более распространенный, связан с наблюдениями Солнца. Предположим сперва, что момент наблюдения - весеннее равноденствие, т. е. Солнце находится в плоскости экватора. Для наблюдателя на экваторе (широта места наблюдения равна 0°) Солнце в полдень находится прямо над головой, т. е. в полдень зенитное расстояние Солнца равно нулю. Если наблюдатель движется от экватора на север, то зенитное расстояние Солнца в полдень возрастает и его величина всегда равна значению широты, на которой находится наблюдатель. На Северном полюсе в полдень во время равноденствия зенитное расстояние Солнца равно 90°, т. е. Солнце только подходит к горизонту, но не поднимается над ним.
В момент равноденствия у Солнца наибольшая скорость в направлении север - юг. Погрешность в вычислении момента равноденствия или при измерении времени дает заметную погрешность при определении широты этим вторым методом. По этой причине обычно используют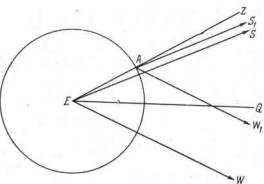 
наблюдения, проведенные в момент солнцестояния, когда Солнце вообще не движется в направлении север - юг.
Рис. III.1.Измерение наклона эклиптики и широты. Линия EQ - экватор. Наблюдатель находится в точке А, и его широта Ж равна углу AEQ. Зенит для наблюдателя находится в направлении AZ. В летнее солнцестояние Солнце находится в направлении ES, в зимнее солнцестояние-в направлении EW. Углы SEQ и WEQ равны наклону эклиптики µ. В летнее солнцестояние наблюдатель видит Солнце в направлении AS1 и угол ZAS1 равен Ж - µ. В зимнее солнцестояние наблюдатель видит Солнце в направлении AW1 и угол ZAW1 равен Ж+µ.
Метод использования солнцестояний показан на рис. III.1. Предположим, например, что наблюдатель находится в 30° северной широты и что наклон эклиптики равен 24°. Тогда точка, расположенная прямо под Солнцем, в летнее солнцестояние находится в 24° северной широты. Следовательно, для нашего наблюдателя Солнце в полдень для летнего солнцестояния находится в 6° к югу от зенита. В зимнее солнцестояние его зенитное расстояние равно 54°. Широта же равна среднему арифметическому этих двух величин.
Если наклон эклиптики считать известной величиной, то наблюдатель может воспользоваться наблюдением только одного солнцестояния. Но в течение почти всего периода греческой астрономии наклон эклиптики не рассматривался как хорошо известная величина, и некоторые наблюдатели думали, что им самим необходимо измерять его одновременно с измерением широты. Как мы видели, широта - это среднее арифметическое (половина суммы) зимнего и летнего зенитных расстояний, а наклон эклиптики равен половине их разности.
Теоретическое выражение, полученное Ньюкомом [Ньюком, 1895] для наклона эклиптики µ, следующее:
µ=23,452 294°-0,013 012° 5Т -0,000 001 64°Т2+0,000 000 503°Т3, (III.1)
где Т обозначает время, измеренное в столетиях, от полудня 0 января 1900г., время гринвичское. В -225г. Т =-21,25 и µ=23,723242° (=23°43'23,7"), а в 1900 г. наклон эклиптики составлял всего лишь 23,452294° (23°27'8,3"). С -225г. наклон эклиптики уменьшился немного больше, чем на четверть градуса.
Я взял для примера -225 г., потому что к этому времени относятся самые знаменитые греческие измерения наклона эклиптики. Сделаны они были астрономом и географом Эратосфеном (годы жизни приблизительно с -275 по -195). Родом он был из Кирены [Дрей-ер, 1905, с. 174], учился в Александрии и в Афинах, затем поселился в Александрии. Труды его, за исключением нескольких отрывков, утеряны, и мы знаем о них в основном по цитатам и комментариям, которые можно найти у других авторов. Нам неизвестно, каким инструментом пользовался Эратосфен для проведения своих измерений. О его результате сказано лишь следующее: Эратосфен получил, что разница между высотами Солнца в летнее и зимнее солнцестояния равна 11/83 полного круга; таким образом он находит, что наклон эклиптики равен 11/166 круга, или 23,855° (=23°51'20''). Как мы видим, по сравнению с приведенной выше величиной ошибка у Эратосфена составляет почти 8', а это примерно половина радиуса видимого диска Солнца. Конечно, нужно поставить вопрос о том, как могли быть проделаны такие измерения. В более позднее время обычным устройством для такого рода измерений у греков был стенной квадрант. Стенной квадрант - это четверть круга, закрепленная так, чтобы она находилась в плоскости меридиана. Сначала подвешиваем из центра отвес и отмечаем, где нить отвеса пересекает круг; так получаем вертикаль. Затем размечаем круг в градусах или в других удовлетворяющих нас единицах. Наконец, в центре помещаем небольшой штырек, тень от которого в полдень попадает на деления и показывает высоту Солнца.
Если пользоваться этим прибором достаточно аккуратно, то можно найти наклон эклиптики с погрешностью в 2' или 3'. По размерам погрешности у Эратосфена можно предположить, что он пользовался более древним инструментом так называемым гномоном (рис. III.2).
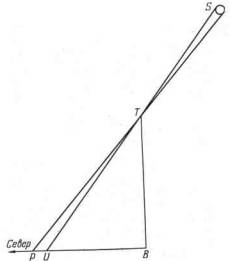
Рис. III.2. Устройство гномона. Гномон - это вертикальный шест, представленный на рисунке прямой ТВ, вместе с градуированной шкалой BUP, идущей по некоторой горизонтальной поверхности на север от точки В. Гномон используется для нахождения высоты Солнца над горизонтом. Солнце нельзя рассматривать как точечный источник света. Луч от верхнего края падает на шкалу в точку U, луч от нижнего края - в точку Р. Отрезок UP называется полутенью
Гномон - это просто вертикальный шест, установленный на некоторой плоской горизонтальной поверхности. Кроме того, на поверхности от основания шеста на север нанесена шкала. Если тень попадает на шкалу, то это полдень. Теперь надо измерить длину тени и найти высоту Солнца из прямоугольного треугольника.
По двум причинам квадрант является более совершенным прибором, чем гномон. Во-первых, если наблюдатель допускает ошибку при нахождении вертикального направления при пользовании, квадрантом, то такая ошибка не дает никакой погрешности в наклоне эклиптики, хотя и даст погрешность при определении широты. Ошибка, допущенная при нахождении вертикального направления, сводится на нет при вычитании показаний полученных в летнее и в зимнее солнцестояния, но при вычислении среднего арифметического, которое дает широту, эта ошибка остается. Если же наблюдатель ошибается при вертикальной установке гномона, то это по-разному сказывается на показаниях прибора в летнее и в зимнее время, так что получаем погрешность и в наклоне эклиптики, и в широте.
Во-вторых, тень, которую отбрасывает штырек, установленный в центре квадранта, симметричная и наблюдатель не получает систематическую погрешность при считывании углов. Тень, отбрасываемая гномоном, как это видно на рисунке, не симметричная, т. к. Солнце не является точечным источником света. Луч от верхнего края Солнца попадает на горизонтальную поверхность в точку U, а луч от нижнего края попадает в точку Р. Часть шкалы между точками В и Uполностью затемнена, часть шкалы, находящаяся к северу от точки Р, не затемнена вовсе, а на отрезке UPтень от полной в точке Uсходит на нет в точке Р. Размеры этой переходной зоны, называемой полутенью, меняются в зависимости от того, стоит ли Солнце высоко на небе, или же низко.
По шкале надо смотреть значение, соответствующее середине отрезка UP. Однако греческий астроном раннего периода мог и не понимать этого. Отметим также, что определить середину отрезка UP совсем не просто. Итак, при пользовании гномоном ожидаемая погрешность сравнима с видимым радиусом солнечного диска, а этот радиус равен примерно 16'. Так что ошибка в 8', допущенная Эратосфеном при нахождении наклона эклиптики, легко объяснима, если он пользовался гномоном, а не квадрантом или каким-либо другим прибором, показания которого определяются по симметричной тени.
Эратосфен измерил также широту Александрии. Об этом речь в следующем разделе. Здесь же отметим только, что широту он определил с погрешностью, равной 10'. Такую погрешность можно ожидать при пользовании гномоном, но никак не при использовании инструмента с градуированным кругом.
Конечно, размеры ошибок, допущенных Эратосфеном, не доказывают, что он пользовался именно гномоном. Он мог пользоваться, например, четвертью круга очень маленького радиуса, по которому трудно точно считывать показания.
Величина наклона эклиптики у Эратосфена больше, чем получается по теории Ньюкома, а греческие астрономы и до Эратосфена использовали значение 24°1 [2]). Несколько большие (как и у Эратосфена) значения наклона эклиптики получены в измерениях, сделанных в Китае до нулевого года [Нидхэм, 1959, с. 287-291]. Это приводит Нидхэма к предположению, что теория Ньюкома требует пересмотра для времен 2 000 лет тому назад.
К счастью, у нас есть более точная информация о наклоне эклиптики 2 000 лет тому назад, чем та, которую можно извлечь из самих измерений наклона эклиптики, проделанных астрономами того времени. Мы располагаем приблизительно восьмьюдесятью измерениями склонений [3]) различных звезд, сделанных греческими астрономами между -290 и 140 годами. По этим измерениям мы можем найти расположение плоскости экватора на -114 г. (середина промежутка от -290г. до 140 г.) и, следовательно, можем рассчитать наклон эклиптики, соответствующий этому времени [Ньютон, 1974]. В результате мы получаем 23°43'±3', что существенно меньше, чем дают измерения, проделанные в то время; кроме того, полученное значение хорошо согласуется с теорией Ньюкома. Итак, нет оснований подозревать, что в теории Ньюкома имеется большая ошибка.
Интересно отметить, что греческие астрономы, насколько я знаю [4]), так никогда и не улучшили значение, найденное Эратосфеном. Именно это значение использовалось в греческой астрономии на протяжении более чем семи столетий, и именно его греческая астрономия завещала своим последователям.
Греческие астрономы могли довольно просто определить широту точки на поверхности Земли, но получилось так, что им были известны широты лишь нескольких мест. Причина в том, что до конца периода греческой астрономии во многих местах измерения так и не были проведены. Широты нескольких мест в Египте, широты Родоса, Афин и немногих других мест - вот, вероятно, и все, что было тщательно измерено, скажем к 500 г.
