2. Точность координат звезд
Погрешности в астрономических данных из всех древних источников, которые я анализировал, имеют одно общее свойство. Начертим некоторую схему, называемую гистограммой; гистограмма показывает частоту, с какой встречаются погрешности разных размеров. Рис. IX.2 - это гистограмма для значений склонений, которые дает Гиппарх в «Комментарии» [Гиппарх, ок. -135]. За погрешность я брал разность между величиной склонения у Гиппарха и величиной склонения, вычисленной по современным данным. Иногда интересно рассмотреть симметрию погрешностей относительно нуля. Но в данном случае мы этого не делаем, так что здесь под «погрешностью» читатель должен понимать «абсолютное значение погрешности».
Предположим, что на рис. IX.2 цена деления по горизонтальной оси равна 0,1°. Если величина погрешности попадает в какой-нибудь интервал между делениями, то в центре этого интервала я ставлю вертикальную отметку. Если там уже есть вертикальная отметка, то новую отметку я делаю на конце старой. При этом я стараюсь все отметки сделать одинаковой длины. В нашем случае 9 погрешностей попадают на интервал между 0° и 0,1°, 8 погрешностей лежат между 0,1° и 0,2° и т. д. [1]).
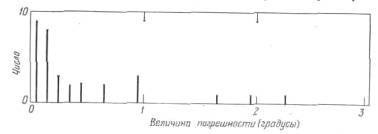Рис. IX 2. Гистограмма погрешностей тех склонений, которые приводит Гиппарх в своем «Комментарии к Арату и Евдоксу». Наиболее правдоподобное объяснение такой картины состоит в том, что погрешности примерно до 0,3° - это случайные погрешности измерения, а погрешности большего размера - это описки в подлиннике или возникающие при его переписывании
Число погрешностей размерами до 0,3° уменьшается по мере возрастания погрешности примерно так, как и должно быть для случайных погрешностей наблюдения. Но для погрешностей больше 0,3° это не так. В этом случае число погрешностей почти не уменьшается с увеличением их размеров. А такое число погрешностей больших размеров нельзя объяснить никаким разумным процессом измерения. Я думаю, каждый статистик без колебания скажет, что погрешности на рис. IX.2 принадлежат двум совокупностям с различным происхождением и различными свойствами.
Наиболее правдоподобное объяснение гистограммы, изображенной на рис. IX.2, состоит в том, что погрешности меньше 0,3° являются случайными погрешностями наблюдения, а погрешности больше 0,3° происходят из-за ошибок в записи. При этом ошибиться в записи результата наблюдения мог и сам наблюдатель. Но даже если он записал результат верно, мы не должны забывать, что работу Гиппарха переписывали в течение почти двух тысячелетий, с одной рукописной копии делали новую рукописную копию. Если в том манускрипте, который копировали, была неверно или непонятно написана буква в слове, то переписчик мог ее исправить. Если же неверной или трудно различимой была цифра, то переписчик не имел никакой возможности исправить ее, поскольку, с его точки зрения, числовые значения могли быть любыми. Для простоты я называю такие ошибки и в подлиннике, и в дошедших до нас экземплярах ошибками записи. Если и можно определить, то только в очень редких случаях, была ли ошибка сделана автором или же все известные экземпляры унаследовали ее от какой-то копии.
На рис. IX.2 показан еще и третий тип погрешности, который не часто встречается в астрономических работах. В четырех случаях Гиппарх не дает точное значение. Он говорит только, что склонение примерно равно такой-то величине; как ясно из контекста, он округляет значение до подходящего целого числа градусов. Однако это не объясняет наибольшую ошибку, равную 3°. Такая погрешность получилась для звезды m Дракона. Гиппарх говорит, что звезда находится в 34 3/5 градуса от полюса, а правильное значение близко к 31 3/5 градуса. В древнегреческих цифрах легко было спутать 1 и 4, и я уверен, что это ошибка записи [2]).
Внимательно сравнивая различные рукописи, часто можно обнаружить ошибки, получившиеся в результате многократного переписывания, и исправить их. Петере и Кнобель тщательно изучили звездный каталог из «Синтаксиса» и, возможно, их версия этого каталога наиболее точная из всех имеющихся (см. Петере и Кнобель, 1915]. Изредка, путем сравнения различных частей одной и той же работы, можно исправить ошибку, допущенную автором в оригинале рукописи; такой пример мы увидим в разделе IX.5.
Поскольку у нас нет никакого способа четко отделить погрешности наблюдения от ошибок записи, мы не можем дать точную оценку размеров погрешностей наблюдения. Но при любом приемлемом разделении ошибок на погрешности наблюдения и ошибки записи мы получим примерно одинаковые оценки. Разделив ошибки вполне допустимым способом, я оценил среднее квадратичное отклонение погрешностей наблюдения на шести множествах данных о звездах; результаты приведены в таблице IX.1. В первом столбце назван наблюдатель, второй столбец дает письменный источник, в котором данные дошли до нас, в третьем столбце названа наблюдаемая величина, и последний столбец дает получившееся среднее квадратичное отклонение погрешностей наблюдения (в минутах дуги).
Таблица IX.1
Точность измерения координат звезд
|
Наблюдатель
|
Источник
|
Наблюдаемая величина
|
Среднее квадратичное отклонение, минуты дуги
|
|
Гиппарх
|
Птолемей а
|
долгота
|
22,3
|
|
Гиппарх
|
Птолемей а
|
широта
|
20,8
|
|
Гиппарх
|
Гиппарх б
|
склонение
|
12,3
|
|
Тимохарис и Аристилл
|
Птолемей а
|
склонение
|
8,8
|
|
Гиппарх
|
Птолемей а
|
склонение
|
6,6
|
|
Птолемей
|
Птолемей а
|
склонение
|
7,2
|
а Птолемей [ок. 142]; б Гиппарх [ок. - 135]
Первые две строки относятся к долготам и широтам звезд в звездном каталоге из «Синтаксиса». Хотя этот каталог имеется в «Синтаксисе», и, как утверждает Птолемей, он сам проводил все наблюдения, в дальнейшем станет ясно, что никаких наблюдений Птолемей не проводил. Почти наверное те наблюдения, которые Птолемей в «Синтаксисе» приписывает себе, провел Гиппарх [3]), и поэтому в таблице IX.1 наблюдателем я назвал Гиппарха.
Последние четыре строки соответствуют четырем множествам измеренных склонений; все они будут рассмотрены в этой главе немного позже. Мы видим, что погрешность в склонениях примерно в два раза меньше погрешности в долготе и широте. Я думаю, это заложено в методике измерения. Склонение можно измерить с помощью градуированного круга, расположенного в плоскости меридиана. Нулевую отметку на этом круге надо сместить от вертикали на географическую широту места наблюдения. Вот и все, что нужно для определения склонения. А широты и долготы определяются с помощью прибора типа астролябии (описание дано в разделе VII.1). Именно этим инструментом Птолемей, как он сам утверждает, пользовался при изучении движения Луны и измерении координат для своего звездного каталога. Прежде чем пользоваться астролябией, ее основные круги должны быть установлены один параллельно, другой перпендикулярно эклиптике, а затем надо быстро считывать показания широты и долготы, пока вращение Земли не нарушит настройку прибора. Неудивительно, что погрешности в долготе и широте вдвое больше, чем для склонения. При получении оценок средних квадратичных отклонений долгот и широт (таблица IX. 1) я использовал координаты не всех звезд из каталога. Для этого есть две причины. Во-первых, на высоких широтах незначительная погрешность наблюдения приводит к большой погрешности в долготе звезды. Во-вторых, в каталоге более 1000 звезд и слишком трудоемкое занятие все их использовать для оценки погрешности. По этим причинам оценки из таблицы IX.1 я получил только по звездам двенадцати зодиакальных созвездий. После того как я отбросил все, что казалось мне ошибкой записи, у меня осталось около 320 звезд. При составлении таблицы IX.1 я пользовался версией каталога из книги Петерса и Кнобеля [1915].
Наблюдения Тимохариса и Аристилла проводились в Александрии около -290 г. Птолемей проводил свои наблюдения также в Александрии около +140 г. Интересно отметить, что за прошедшие четыре века не было получено никакого значительного улучшения точности. В предыдущих главах то же самое мы получали для других типов наблюдений. Точность любых греческих наблюдений оставалась, по-видимому, примерно одинаковой от самых первых известных нам наблюдений и до самых последних.
