2. Ќаибольшие элонгации
†
ћы уже провели в предыдущих главах достаточно длинные обсуждени€ наибольших элонгации ћеркури€ и ¬енеры, поскольку в теории ѕтолеме€ измерени€ наибольшей элонгации играют главную роль при нахождении параметров орбит этих планет. ¬ частности, мы видим, что наибольша€ элонгаци€ неравномерна по орбите, т. е. наибольша€ элонгаци€ зависит от значени€ LШ в тот момент, когда она достигает максимума.
ѕтолемей обращаетс€ к этим вопросам в главах XII.9 и XII.10. Ќо здесь он имеет дело с элонгацией от действительного —олнца, а не от среднего, как он подразумевал до сих пор. ѕричина в том, что элонгацию от среднего —олнца он использует г, теоретической работе, а элонгаци€ от действительного —олнца - это то, что интересно само по себе как наблюдаемое €вление. «аканчивает данную часть своей работы ѕтолемей таблицей, по которой можно определить и дл€ ћеркури€, и дл€ ¬енеры наибольшую восточную и наибольшую западную элонгации как функции LШ.
я не пыталс€ внимательно следить за этой частью труда ѕтолеме€, но его таблица обнаруживает интересную черту. —умма восточной и западной элонгации дл€ одного и того же значени€ LШ равны всему углу, ст€гиваемому эпициклом. ћы использовали этот факт, например, при анализе рис. ’.6. Ётот суммарный угол равен углу, под которым Ђвиденї эпицикл, если смотреть из точки, обозначающей положение «емли. ѕоэтому он зависит от рассто€ни€ «емл€ - центр эпицикла. огда центр находитс€ в максимальном удалении (а ѕтолемей называет это апогеем ћеркури€ или ¬енеры), Ђвидимыеї размеры эпицикла минимальны. огда центр расположен ближе всего к «емле (по терминологии ѕтолеме€ это перигей), Ђвидимыеї размеры эпицикла достигают максимума.
†
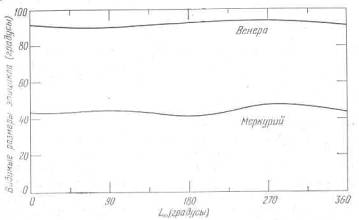 –ис. XII.2. Ђ¬идимыеї размеры эпициклов ћеркури€ и ¬енеры (полученные по теории ѕтолеме€) как функции LШ. ѕравильный график дл€ ћеркури€ имеет единственный максимум и единственный минимум, но теори€ ѕтолеме€ приводит к двум максимумам и двум минимумам
–ис. XII.2. Ђ¬идимыеї размеры эпициклов ћеркури€ и ¬енеры (полученные по теории ѕтолеме€) как функции LШ. ѕравильный график дл€ ћеркури€ имеет единственный максимум и единственный минимум, но теори€ ѕтолеме€ приводит к двум максимумам и двум минимумам
†
†
†
†
Ќа рис. XII.2 € изобразил Ђвидимыеї размеры эпицикла (сумма восточной и западной элонгации по теории ѕтолеме€) как функцию средней долготы —олнца LШ. «ависимость получена и дл€ ћеркури€, и дл€ ¬енеры. рива€ дл€ ¬енеры имеет единственный максимум и единственный минимум, как и должно быть. ј вот крива€ дл€ ћеркури€ имеет два максимума и два минимума.
–ис. ’.10 также показывает зависимость Ђвидимыхї размеров эпицикла ћеркури€ от значений LШ, но дл€ построени€ этих кривых размеры вычисл€лись не по теории ѕтолеме€, а по современной теории. ћы видели, что должен быть единственный максимум и единственный минимум, а не по паре экстремумов, как на рис. XII.2. — другой стороны, ѕтолемей так строит свою теорию, что в ней должно быть одно положение апоге€ и два положени€ периге€, а между двум€ положени€ми периге€ должна быть точка, в которой рассто€ние имеет локальный минимум. Ќо этот локальный минимум должен быть меньше того рассто€ни€, какое соответствует птолемееву апогею.
” ѕтолеме€ апогей достигаетс€ при LШ=190∞, и Ђвидимыеї размеры эпицикла должны быть (здесь минимальными. ƒругой минимум должен быть при LШ=10∞, но этот минимум будет не таким Ђглубокимї, как при 190∞. рива€ на рис. XII.2 все это вы€вл€ет. ћаксимумов должно быть два. ќни соответствуют птолемеевым точкам периге€. ћаксимумы должны быть равны и расположены симметрично относительно точки апоге€ с долготой, равной 190∞. ћы видели, что два максимума равноудалены от точки с долготой 190∞, но Ђвидимыеї размеры в этих двух максимумах совсем не одинаковые.
»з таблицы ’.1 мы видим, что при LШї70∞ имеетс€ максимум и это ошибка [1]). ѕри LШ=310∞ Ђвидимыйї диаметр эпицикла равен сумме элонгации из наблюдений 1 и 4, т. е. 47;45 градуса. Ёто прекрасно согласуетс€ с кривой на рис. XII.2. Ђ¬идимыйї диаметр при LШ=70∞ равен сумме элонгации дл€ наблюдений 2 и 3, и это тоже равно 47;45 градуса, а рис. XII.2 показывает, что угол, под которым Ђвиденї с «емли диаметр эпицикла, меньше 45 градусов.
Ѕыло бы интересно вы€вить происхождение полученного расхождени€ путем тщательного изучени€ всего того, что делает ѕтолемей в главах XII.9 и ’II.10 Ђ—интаксисаї. Ќо € не стану заниматьс€ здесь такими исследовани€ми, чтобы не увеличивать и без того достаточно большую по объему книгу.