ПРЕСТУПЛЕНИЕ КЛАВДИЯ ПТОЛЕМЕЯ

СОДЕРЖАНИЕ
Предисловие редактора перевода

Предисловие автора

Глава   I. Объяснение явлений в астрономии

Глава   II. Греческая математика

Глава   III. Земля

Глава   IV. Строение мира

Глава  V. Солнце и связанные с ним вопросы

Глава   VI. Долгота полной Луны

Глава   VII. Долгота Луны в любой фазе

Глава  VIII. Размеры Солнца и Луны. Расстояния до них

Глава   IX. Звезды

Глава   X. Движение Меркурия

Глава   XI. Венера и внешние планеты

Глава   XII. Некоторые второстепенные вопросы

Глава   XIII. Оценка деятельности Птолемея

Приложение А. Специальные термины и обозначения

Приложение Б. Метод Аристарха для нахождения размеров Солнца

Приложение В. Как Птолемей пользовался вавилонским календарем

Список литературы

3. Модель Птолемея, описывающая движение Луны

 

Еще за три столетия до Птолемея Гиппарх нашел, что Е (максимальное значение уравнения центра для Луны) значительно больше в квадратурах, чем в новолуние или полнолуние. Таким образом, Гиппарх открыл эвекцию как наблюдаемое явление. Птолемей гово­рит [глава V.3 «Синтаксиса»], что он получил то же самое из наблюде­ний, проведенных с помощью астролябии. После этого Птолемей при­водит описание наблюдения (в предыдущем разделе оно стоит под номером 1), где записано, что действительное положение Луны было в 7 2/3 градуса за положением средней Луны.  Наблюдение проведено 9 февраля 139 г., когда Луна находилась в последней четверти.

Дальнейшие действия Птолемея сильно отличаются от того, как он поступал с лунными затмениями и как он находил Е для полнолу­ний. Птолемей считает, что Гиппарх не смог правильно проанализиро­вать наблюдения и на его результаты полагаться не следует. И здесь, же подчеркивает согласованность своих результатов с тем, что получил Гиппарх. 5 августа -127 г. Гиппарх наблюдал Луну в последней чет­верти (в предыдущем разделе это наблюдение стоит под номером 2) и также получил, что действительное положение отличалось от сред­него на 7 2/3 градуса, но только в этом случае действительное положе­ние было «перед» средним, а не «за» ним.

Если взять радиус деферента равным единице, то максимальное зна­чение уравнения центра равно arcsin r (уравнение (VI.11)). Если же радиус деферента равен R, то

E=arcsin (r/R). (VII.1)

Если в квадратуре максимум Е больше, чем в сизигии, то, соответст­венно, должно быть больше и отношение r/R. Птолемей подчеркивает это соображение в последнем предложении главы V.2 «Синтаксиса». И затем, как оказалось, он делает грубую ошибку. Птолемей говорит, что поскольку радиус эпицикла r - константа, то радиус деферента R должен для фазы четверти быть меньше, чем для сизигий [1]).

Если мы согласимся с Птолемеем, то легко найдем отношение между значениями R в четвертях и в сизигиях. В сизигиях sin E=5;15 : 60=0,0875. В квадратурах [2])  Е=7 2/3 градуса и sin E= 0,133410. Отношение равно 0,0875/0,133 410=0,655873, так что если в сизигиях R=60, то в квадратурах Rдолжен быть 39,35 (или 39;21 в шестидесятеричных обозначениях). Для своей окончательной модели Птолемей берет значение 39;22. Теперь Птолемею нужно, используя равномерное движение по окружности, объяснить изменение радиуса деферента с 60 в новолуние до 39;22 в первой четверти, обратно до 60 в полнолуние, снова до 39;22 в последней четверти и до 60 в следующее новолуние. Схема Птолемея показана на рис. VII.2. На этом рисунке точка Е обозначает центр Земли, ^-направление на весеннее равно­денствие,  - направление на среднее положение Солнца. Угол ^Е - это средняя долгота Солнца, угол ^E - средняя долгота Луны, оба эти угла равномерно возрастают.

Прямая Е равномерно вращается вокруг точки Е, при этом длина Е меняется. В то время как Е вращается вокруг точки Е против часовой стрелки, другая прямая ЕС₁ с той же скоростью так вращается вокруг точки Е по часовой стрелке, что углы `M Eи C₁E всегда рав­ны между собой и равны средней элонгации DЛуны от Солнца. По­стоянные расстояния ЕС₁ и С₁ нужно определить из исходных дан­ных. Давайте на время забудем о других элементах рис. VII.2 и пусть Р обозначает расстояние С₁ [3]), а Б - расстояние ЕС₁.

Следуя Птолемею, считаем радиус деферента равным 60. Схема Птолемея для новолуния и первой четверти показана на рис. VII.3. В новолуние D=0, а Б и Р имеют направление на среднее положение Солнца . В первой четверти D=90°. Тогда Б лежит справа от точки Е, а Б слева отточки С₁. В новолуние радиус деферента равен Р+Б =60. В первой четверти радиус деферента равен Р - Б =39;22. Следова­тельно,

Р = 49;41,    Б = 10;19.            (VII.2)

Радиус эпицикла М (мы обозначаем его r) равен 5;15.

На рис. VII.3 радиус эпицикла М и для новолуния, и для первой четверти нарисован в таком положении, которому соответствует максимальное значение уравнения центра. Видно, что максимальное зна­чение уравнения центра (угол, стягиваемый радиусом эпицикла) на самом деле в квадратурах больше, чем в новолуние.

Таким способом эвекцию можно описать  только в  сизигиях и в квадратурах, и ни в

 

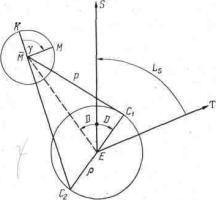
Рис. VII2. Система эпицикл - деферент, ко­торую Птолемей использует для Луны. ^ - направление от Земли на точку весеннего равноденствия,  - направление на среднее Солнце,  - среднее положение Луны, угол ^E - средняя долгота Луны. Угол E - средняя элонгация D, возрастающая в на­правлении против часовой стрелки. Прямая С₁ЕС₂ поворачивается вокруг прямой E по часовой стрелке таким образом, что величина угла С₁E равна D. Bо время движения точ­ки М расстояние С₁М остается постоянным. Расстояния EC₁ и ЕС₂ равны. Средняя анома­лия і измеряется от луча К (продолжение С₂) по часовой стрелке. Точка М - дей­ствительное положение Луны.

 

 

 

 

 

 

 

 

 

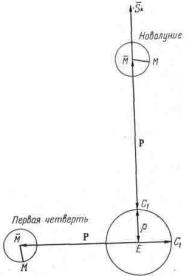
Рис. VII.3. Птолемеева модель движения Луны. Конфигурации для новолуния и первой четверти. В новолунии расстояние Е равно Р+Б, а в первой четверти Р-Б. Обозначения здесь такие же, как на рис. VII2. В обоих случаях рас­стояние по долготе между точками М и  наибольшее. Конфигура­ции для полнолуния и последней четверти симметричны конфигура­циям на этом рисунке. Масштаб примерно выдержан.

 

 

 

 

какой другой фазе. С точки зрения современных методов это особенно хорошо видно, если в уравнении (VI.4) оставить два старших члена, описывающих энекцию, и оценить их в какой-либо другой фазе, скажем, при D=45°. Два старших члена в уравнении (VI.4) дадут нам

6,29° sin M+1,27° cos M,

и это выражение не обращается в нуль при М = 0, если мы измеряем М от прямой, соединяющей точки Е и . Для того чтобы получить лен 1,27° cos M, мы должны измерять М от некоторого другого на­правления.

Птолемей, конечно, пользовался совсем другими терминами. На­сколько известно, он не мог и подозревать о верном математическом описании эвекции. Птолемей из наблюдений определяет, что требует­ся дальнейшее развитие схемы. Для этого он использует измерения, полученные из наблюдений 2 мая -126 г. и 7 июля -126 г. (см. табли­цу VII. 1), которые приписывает Гиппарху [глава V.5 «Синтаксиса»].

Наблюдение 2 мая -126 г. проведено посредине между последней четвертью и новолунием, когда средняя элонгация Dравнялась 315;32 градуса по расчетам Птолемея и 315;34 по моим расчетам. Ситуация отображена на рис. VII.4 (масштаб примерно выдержан). Чтобы не загромождать рисунок, мы не отметили точку , являющуюся цент­ром эпицикла, расположенного в правом верхнем углу. Другие обоз­начения имеют тот же смысл, что и на рис. VII.2. Поскольку прямая Е вращается против часовой стрелки, то точка  находится в 315° «впереди» среднего положения Солнца  [4]). Средняя аномалия Луны по вычислениям Птолемея равнялась 185;30 градуса, а по моим 185;28. Если, как и раньше, измерять аномалию от точки Z (эта точка лежит на продолжении линии Е), то Луна должна была появиться немного слева от  (за недостатком места Луну на рисунке я не отметил). Лу­на должна была быть впереди среднего положения Луны, и уравнение центра должно было быть положительным.

Измеренная долгота Луны была равна 351;27,30 градуса (см. таб­лицу VII.1). Долгота L₍ средней Луны по вычислениям Птолемея была равна 352;13 градуса и 352;10 градуса по моим вычислениям. Следова­тельно, уравнение центра е_С равно -0;45,30, если брать числа, полу­чившиеся у Птолемея. Сам он сразу заменяет это значение на -0;46. Замена вполне допустимая. Но тогда Луна находится справа от прямой EZ, а не слева. Из наблюдения мы можем определить, где на эклип­тике находится Луна, и от ее положения измерить по эпициклу вели­чину аномалии (185;30 градуса) до точки K. Затем продолжаем прямые К и C₁E до их пересечения в точке С₂ и вычисляем расстояние ЕС₂. В том масштабе, в каком даны равенства (VI 1.2), расстояние ЕС₂ рав­но 10;18. Сам я вычислений до конца не проводил и поэтому мне не с чем сравнивать, но с уверенностью могу сказать, что, насколько поз­воляет ситуация, вычисления Птолемея точны.

Путем измерений Птолемей показал, что с высокой степенью точ­ности расстояния EС₁ и ЕС₂ равны. Он проверяет это и по наблюде­нию 7 июля -126 г. В момент этого наблюдения элонгация Луны D(угол E) почти точно равнялась 45°. Конфигурация, показанная на рис. VII.5, по существу, зеркальное отражение рис. VII.4. Для наблюдения 7 июля -126 г. я сейчас приведу только те значения, ко­торые получил из расчетов Птолемей.

Долгота Луны, полученная из измерений, была равна 148;46 гра­дуса, долгота средней Луны была равна 147;20 градуса. Следователь­но, е_С= + 1;26 градуса. Средняя долгота была равна 333;12 градуса. Если бы это значение получилось при измерении средней аномалии по

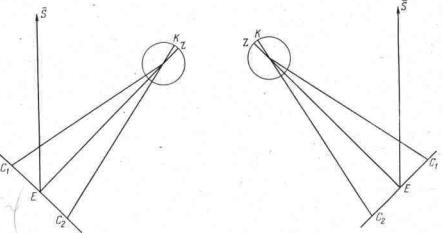
Рис. VII.4. Птолемеева модель движе­ния Луны. Конфигурация для наблю­дения 2 мая -126 г. С Земли Луна бы­ла видна немного правее линии EZ, а средняя аномалия была равна 185,30 градуса. Следовательно, среднюю ано­малию надо измерять не от точки Z, a от точки К.

Рис. VII.5. Птолемеева модель движе­ния Луны. Конфигурация на время наблюдения 7 июля - 126 г. С Земли Луна видна немного слева от линии EZ, но ее положение не согласуется со значением средней аномалии, которая равна 333,12 градуса. Среднюю ано­малию надо измерять от точки К, а не от точки Z.

 

часовой стрелке от точки Z, то е_С равнялось бы +2;33, а не 1;26 граду­са; так что средняя аномалия должна была измеряться от другой точ­ки. Положения эпицикла, точки К (для нахождения точки К мы от­меряем на эпицикле величину средней аномалии) и точки С₂ опреде­ляются так же, как и раньше. Птолемей находит, что расстояние EС₂ равно 10;20.

Заканчивая рассмотрение подобной ситуации, Птолемей из наблю­дений 9 февраля 139 г. и 5 августа -127 г. находит, что в его масштабе расстояние ЕС₁ равно 10;19. Из наблюдения 2 мая -126 г. он нахо­дит, что ЕС₂ равно 10;18, а из наблюдения 7 июля -126 г. он получает, что EС₂ равно 10;20.

 

---