Глава VII.2

2. Ранние исследования расстояний до Солнца и Луны

За несколько столетий до Птолемея у греческих астрономов были достаточно хорошие оценки размеров Луны и расстояния до нее, по крайней мере, если за единицу измерения взять радиус Земли [1]). Знали они также, что Солнце намного больше Земли и подавно намного больше Луны, хотя их оценки были далеки от правильных.

Мы не знаем всех методов, которыми греческие астрономы пытались оценить эти величины, но два основных метода нам известны. Один из них прямо дает нам отношение расстояний до Солнца и до Луны. В другом методе мы получаем сумму горизонтальных параллаксов Солнца и Луны. Из этих соотношений мы можем найти оба расстояния. Затем, измерив видимые диаметры солнечного и лунного дисков, мы сможем вычислить физические размеры Солнца и Луны (при этом мы предполагаем, что они, как и Земля, являются сферическими объектами).

Первым методом пользовался Аристарх Самосский, астроном, предложивший гелиоцентрическую теорию солнечной системы. Данный метод описан в единственной дошедшей до нас работе Аристарха [Аристарх, ок.-280]. Хит, который перевел и подготовил к печати эту работу Аристарха, в своей книге [Хит, 1913] приводит также и информацию, полученную из других астрономических работ греков по данному вопросу.

Метод определения отношения расстояний показан на рисунке VIII.1. Если мы видим ровно половину диска Луны, то прямая из центра Луны к центру Земли перпендикулярна прямой, соединяющей центры Луны и Солнца. Более точно, следует говорить о прямой, идущей к точке наблюдения, поскольку на результаты очевидным образом влияет параллакс. Если наблюдатель, для которого Луна находится в . меридиане точки наблюдения (другими словами, на рисунке наблюдатель находится на прямой, соединяющей центры Луны и Земли), видит ровно половину диска Луны, то наблюдатель, находящийся около точки Е (рис. VIII.1), видит больше половины диска Луны, а наблюдатель, находящийся на противоположной стороне Земли, видит меньше половины лунного диска.

Если не учитывать параллакс, то можно сказать, что отношение расстояния до Солнца к расстоянию до Луны равно секансу угла D,

элонгации Луны в момент наблюдения. Аристарх брал значение D равным 87° [2]), так что отношение было равно

sec 87°= 19,1073. (VIII.1)

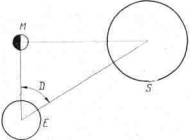
Рис. VIII.1. Метод нахождения отношения между расстояниями до Солнца и до Луны. Когда Луна точно в квадратуре, направления от нее к Земле и к Солнцу перпендикулярны. Отношение расстояния до Луны к расстоянию до Солнца равно косинусу элонгации D. Рисунок воспроизведен из Части I с разрешения Quarterly Journal of the RAS

Аристарх, конечно, не использует понятия секанса. Не говорит он и что отношение было равно 19, хотя прежде всего можно было бы ожидать именно такую формулировку. Аристарх говорит, что значение отношения находилось между 18 и 20. Это не похоже на способ выразить неуверенность в результатах наблюдения; такая формулировка порождена, очевидно, ограниченностью его знаний о тригонометрических функциях [3]). Для простоты при обсуждении результатов Аристарха я буду пользоваться равенством (VШ.1), но читатель должен помнить, что у Аристарха его нет.

В книге Дрейера [1905, с. 182] приведено несколько значений отношения расстояния до Солнца к расстоянию до Луны, которыми пользовались греческие астрономы. Какими способами они получали эти значения, мы не знаем. А значения получались разные: от 9 до 30. Правильное значение отношения около 400, так что все их оценки сильно занижены. И все же все они приходили к правильному выводу, что Солнце намного больше Земли.

Приведем пример. Пусть среднее значение расстояния до Луны равно 60 (это близко к правильному значению). Тогда расстояние до Солнца равно 60*19,1073=1 146. Видимый радиус солнечного диска равен примерно четверти градуса. Получаем, что физический радиус Солнца почти точно равен пяти радиусам Земли, а объем Солнца в 125 раз больше объема Земли. Это значение меньше значения, полученного Аристархом. Он говорил, что значение отношения объемов лежит между 6 859/27(=254) и 79 507/216(=368).

Метод нахождения суммы параллаксов Солнца и Луны показан на рис. VIII.2. Круги с центрами в точках S и Е - это Солнце и Земля, прямая ABV показывает край тени Земли [4]). Дуга ММ.' - часть круга, радиус которого равен расстоянию до Луны. Предположим, что на расстоянии ЕС помещен большой экран. На экране мы получим проекцию тени и угол CEV будет равен видимому с этого расстояния (расстояние до Луны) радиусу тени Земли. Этот радиус (угол) я обозначаю Б_U_.

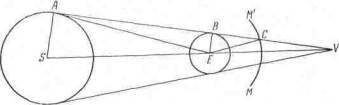
Рис. VIII.2. Метод нахождения суммы параллаксов Солнца и Луны. Точки S и E- центры Солнца и Земли. Линия ММ' - часть круга, радиус которого равен расстоянию до Луны. В основе этого метода лежит тот результат из элементарной геометрии, согласно которому сумма углов AES и CEVравна сумме углов ВАЕ и ВСЕ. Этот рисунок воспроизведен из Части 1 с разрешения Quarterly Journal of the RAS

Можно дать интерпретацию и другим углам на рис. VIII.2. Так, угол AES - видимый радиус Б солнечного диска. Угол ЕАВ - параллакс Солнца, т. е. разница тех направлений, в которых точка А на Солнце видна из точек Е и В [5]). Аналогично, угол ЕСВ - параллакс Луны. Из элементарной геометрии получаем

Р AES + Р CEV = Р ЕАВ + Р ЕСВ.

Если же воспользоваться астрономической интерпретацией этих углов, то получим

Б + Б_U= П + П₍. (VIII.2)

Видимый радиус Б Солнца измеряем непосредственно, а радиус тени Б_U можно получить во время частного лунного затмения. Немного позже я объясню, как это делается. Подставив найденные значения в уравнение (VIII.2), мы получим сумму параллаксов, а равенство (VIII.1) дает нам отношение этих параллаксов [6]). Решая систему двух уравнений, мы находим оба параллакса, а следовательно, и оба расстояния: и до Солнца, и до Луны. Единицей измерения расстояния в этом случае служит радиус Земли.

Прочитав различные изложения работы Аристарха и комментарии к ней, я нахожусь в некотором замешательстве относительно того, что же он делал. Частично причиной тому служит его способ изложения материала. Начинает Аристарх с формулировки шести предположений [7]):

1. Луна получает свой свет от Солнца.

2. Землю рассматриваем как точку и центр сферы, по которой движется Луна.

3. Если мы видим половину диска Луны, то большой круг, разделяющий Луну на темную и светлую стороны, расположен в направлении луча зрения.

4. Если видна половина диска Луны, то расстояние [8]) от нее до Солнца меньше квадранта на одну тринадцатую квадранта.

5. Ширина тени (Земли) равна (ширине) двух Лун.

6. Луна стягивает одну пятнадцатую часть знака зодиака.

Первые три предположения нужны для обоснования тех геометрических построений, которыми пользовался Аристарх, и вряд ли он настаивал на буквальном понимании второго предположения. Согласно предположению 4, если мы видим половину диска Луны, то элонгация Луны равна 87°. Предположение 5 говорит о том, что Б_Uв два раза больше Б₍, а предположение 6 говорит нам, что видимый диаметр Луны равен 2°, т. е. Б₍ = 1Ъ.

Затем Аристарх говорит, что из этих предположений он докажет три утверждения:

1. Расстояние от Земли до Солнца больше чем в восемнадцать, но меньше чем в двадцать раз превышает расстояние до Луны.

2. То же самое можно сказать и об отношении диаметров Солнца и Луны [9]).

3. Отношение диаметра Солнца к диаметру Земли больше, чем отношение 19 к 3, но меньше, чем отношение 43 к 6.

Может быть, и есть обсуждения труда Аристарха, которые проясняют, что же он делал, но в тех, которые я видел, сказано, что Аристарх доказывает свои утверждения из своих предположений, и нигде не сказано, что это невозможно. В предположения и утверждения входят пять неизвестных величин. Это диаметры Солнца и Луны, расстояния до Солнца и до Луны и ширина тени Земли (на расстоянии, равном расстоянию от Земли до Луны). Однако в предположения входят только три соотношения между этими пятью величинами и еще одно соотношение получаем из геометрических свойств тени. Пять неизвестных из четырех уравнений найти нельзя. И то, что Аристарх находит все пять величин, объясняется тем, что он неявно вводит еще два соотношения в форме неравенств. Эти дополнительные соотношения и дают недостающую информацию. Более подробное изложение займет много места, и я откладываю его до Приложения Б.

Данные, использовавшиеся Аристархом, содержат две грубые ошибки. Величина, на которую элонгация отличается от квадранта (90°), взята слишком большой, поэтому отношение расстояния до Солнца к расстоянию до Луны получилось слишком маленьким. Правильное значение этой величины близко к 10', а не к 3°. Но учитывая сложность проведения измерений, такая ошибка не вызывает удивления.

Вторую серьезную ошибку мы находим в значении угла, под которым с Земли виден диаметр Луны (предположение 6). Значение, которое дает Аристарх, почти в четыре раза больше правильного. Я встречал три возможных объяснения этому факту.