3. Греческая тригонометрия на плоскости
На рис. II.2 показаны обычные тригонометрические функции. Радиус окружности равен единице, OВ и ОЕ - два перпендикулярных радиуса, BD и EF- касательные, перпендикулярные соответственно OВ и ОЕ, и СA - перпендикуляр из точки С на радиус OВ. Если теперь парой заглавных букв с чертой над ними обозначить длину прямолинейных отрезков (например, 
обозначает длину соответствующего отрезка), то получим такие равенства:
sinё=
, cosecё = 
,
соsё= 
, secё = 
, (II.4)
tgё =
, ctgё =
.
В том случае, если радиус 
не равен единице, эти функции выражаются через отношения длин, т. е. sinё=
/
и т. д.
Задачи о треугольниках, как мы только что видели, греки решали без труда. Интересно, что они это делали с помощью одной лишь тригонометрической функции, которой, кстати, нет среди шести только что определенных. Эта функция называется хордой; иллюстрацией служит рис. II.3. Если радиус окружности равен единице, то 
- хорда угла ±. Нам не часто придется иметь дело с функцией хорды, поэтому можно не вводить специального сокращения для нее, и я буду просто записывать
chord ± =
, (II.5)
Половина хорды
, очевидно, равна sin(1/2(±)), т.е.
chord ± = 2 sin(1/2(±)). (II.6)
Было бы заблуждением считать, что греческие математики знали только одну тригонометрическую функцию. Из рис. II.2 видно, что косинус угла а равен синусу дополнительного угла, т. е. cosё= =sin(90°-ё). Греки знали, что хорда смежного угла - это величина полезная. Но они не дали этой величине своего названия. Более точно, греки пользовались не только хордой угла ±, но и хордой угла І = 180°-±. Однако при этом они не называли хорду угла І чем-то вроде «ко-хорды угла ±». Итак, они использовали хорду угла І тесно связанную с соs(1/2(±)).
Самым большим недостатком греческой тригонометрии на плоскости было отсутствие аналога функции тангенса. Но это неудобство никак не ограничивало умения греков решать задачи с треугольниками. В определении синуса или косинуса (синуса дополнительного угла) участвуют один катет и гипотенуза прямоугольного треугольника, тангенс же определяется двумя катетами. Но, зная оба катета, мы всегда можем найти гипотенузу по теореме Пифагора, не используя никакой информации об углах. Так что углы мы можем найти с помощью только одной функции синуса или хорды, даже если нам известны только катеты.
В главе I.11 Птолемей приводит таблицу хорд для углов от 0° до 180° через каждые полградуса. Это эквивалентно таблице синусов углов от 0° до 90° с приращением в 1/4 градуса. Мы, вероятно, применили бы бесконечные ряды для нахождения значений функции, но греческие математики не знали этого метода. Они начинали с хорд, которые можно определить элементарными построениями. Из свойств равносторонних треугольников и квадратов мы можем получить chord 60° и chord 90°. С помощью циркуля и линейки можно построить правильный пятиугольник и найти chord 72°. Затем последовательным делением углов для каждого целого n можно определить хорды углов 60°/2n, 72°/2n и 90°/2n. Чтобы идти дальше, мы должны уметь находить хорды углов вида (±±І) по известным хордам углов ± и І.
Птолемей делает это с помощью теоремы, которая до сих пор в некоторых геометрических текстах называется теоремой Птолемея. Посмотрим на рис. II.4. Отрезки 
,
,
и 
на рисунке - это стороны четырехугольника, вписанного в окружность. Если через 
обозначить дугу между точками A и В, то получим 
=chord 
. Для трех других дуг можно записать аналогичные равенства. Согласно теореме, доказанной у Птолемея,
* 
= 
* 
+
*
.
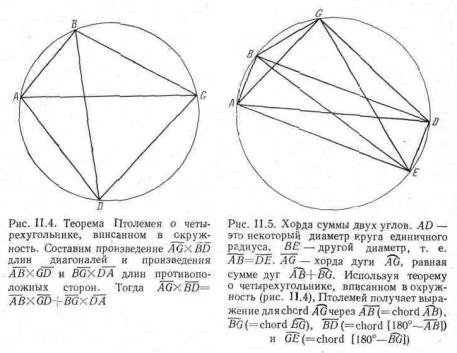
Эту теорему Птолемей применял к четырехугольникам ABGD и ABGE (рис. II.5). В обоих этих четырехугольниках либо диагональ, либо сторона являются диаметром (радиус окружности взят равным единице). Диаметры - это 
и 
, так, что
=
и 
=
. Далее, 
= 180°-
. Ясно, что 
=chord 
=chord (
+
). Я буду пользоваться термином «ко-хорда ±» («co-chord ±») для обозначения хорды угла (180°-±), хотя у греческих математиков такого понятия не было; я ввожу ко-хорду, чтобы подчеркнуть аналогию с привычными для нас формулами. Итак, 
=chord
, 
=
=co-chord
, 
=chord
и 
=co-chord
. Применив теорему к четырехугольнику ABGE, мы получим
2 chord (
+
) = = chord
* co-chord 
+ co-chord 
* chord 
Это аналогично равенству
sin(±+І)=sin ± * cos І+cos ± * sin І.
Из четырехугольника ABGD получим выражение для chord 
=chord(
-
), аналогичное формуле для вычисления sin(±+І). Из элементарной геометрии мы знаем хорды 60°, 72° и 90°. Используя только что полученные теоремы, мы можем теперь найти хорду любого угла, являющегося целым кратным угла 1 1/2 градуса, а также
любого угла, полученного последовательным делением пополам этого угла 1 1/2 градуса. Но хорду 1/2 градуса, которая необходима Птолемею для составления его таблицы, мы получить не можем. Последний этап работы над таблицей Птолемей начинает с использования равенств [1])
chord (1 1/2 градуса)=0;1,34,15, (II.7)
chord (3/4 градуса)=0;0,47,8.
Птолемей пользуется также тем, что
chord ±/chord І<±/І, (II.8)
если ±/І >1. Данное неравенство эквивалентно утверждению о том, что хорды возрастают медленнее, чем углы или дуги. Доказать это можно многими способами [2]).
Сначала Птолемей использует неравенство (II.8) для ±=1°, І =3/4 градуса, а значение chord 3/4 он берет из равенств (II.7). Отсюда получается, что chord1°<(4/3)*0,0,47,8. У Птолемея это записано так:
chord 10<0; 1,2,50. (II.9)
Заметим, что (4/3)*0;0,47,8 равно 0;1,2,50,40, так что неравенство (II.9) не доказано.
Затем Птолемей пользуется неравенством (II.8) для ±=1 1/2 градуса, І = 1° и значение chord 1 1/2 берет из равенств (II.7). Таким образом, chord 10>(2/3)*0;1,34,15. Это Птолемей записывает правильно:
chord 10>0;1,2,50. (II.10)
Сравнение неравенств (II.9) и (II.10), в которых оценки в правых частях не абсолютно точные, ведет к тому, чтобы положить chord 1°=0;1,2,50. Теперь Птолемей может закончить составление своей таблицы.
Птолемею в некотором смысле повезло. Ведь его методы в действительности недостаточно точны для обоснования его выводов. Запишем величины из равенств (II.7) с точностью до четвертого разряда. Тогда в правых частях равенств получим 0;1,34,14,42 и 0;0,47,7,25. Если теперь округлить до третьей позиции, то мы видим, что величина, стоящая в первом из равенств (II.7), правильная, а вторая должна быть равна 0;0,47,7. Повторим все действия, приводящие к неравенствам (II.9) и (II.10), и округлим полученные числа до третьего разряда. Тогда одновременно должны выполняться неравенства
chord 10<0; 1,2,49, chord 10>0; 1,2,50,
что невозможно. Если бы Птолемей считал аккуратно, он понял бы, что получить некоторую величину с точностью до третьего разряда можно, лишь сохраняя в вычислениях точность до следующего разряда. Придерживаясь этого правила, мы найдем
chord 10<0;1,2,49,55,
chord 1°>0;1,2,49,48.
Так что с точностью до третьей позиции после точки с запятой chord 1° действительно равна 0;1,2,50, как и полагал Птолемей. Однако его собственное доказательство неверно.
В главе I.10 «Синтаксиса» Птолемей говорит, что хорду 1/2 градуса непосредственно из хорды 1 1/2 градуса найти нельзя, возможно, потому, что это было равносильно геометрической трисекции угла.
Конечно, с помощью циркуля и линейки решить данную задачу нельзя, но мы можем тем не менее найти хорду 1/2 градуса по известной хорде 1 1/2 градуса. Птолемей знал, как находить chord (±±І), значит, он мог найти chord 2± и chord 3±, т. е. он мог получить результат
chord 3±=3 chord ±-(chord ±)3,
который аналогичен формуле sin3ё=3 sin ё-4 sin3 ё. Из этого соотношения сразу можно получить хорду 1/2 градуса, если угол 3± взять равным 1 1/2 градуса. Такое уравнение Птолемей вполне мог решить. Как показывает практика, для нахождения простейшего способа решения задачи требуется длительное время, так что не будем критиковать Птолемея за то, что он не смог найти этот способ. Пожалеем лишь о том, что его собственный метод неверен.
