4. Греческая сферическая тригонометрия
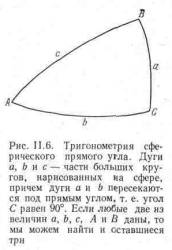Из всей греческой математики еще нам потребуется лишь тригонометрия сферического прямоугольного треугольника. Такой треугольник изображен на рис. II.6. Читатель должен представить себе, что дуги a, b и с - это части больших кругов, проведенных на сфере. Эти дуги назовем сторонами сферического треугольника. Стороны треугольника пересекаются под углами А, В и С; угол С считаем прямым. Ситуация похожа на ситуацию с прямоугольным треугольником на плоскости: если заданы любые две величины (при этом мы знаем, что С=90°), то остальные величины также можно найти. Однако не обязательно, чтобы одной из задаваемых величин была сторона; правда, если заданы только углы, может случиться, что нельзя будет обеспечить хорошую точность при нахождении сторон [1].
Из дошедших до нас греческих работ по сферической тригонометрии наиболее важен, по-видимому, трактат Менелая [Менелай, ок.100]. На языке оригинала эта работа утеряна, и она сохранилась лишь в средневековом арабском переводе, а теперь есть еще и немецкий перевод 1936 г. Основная теорема, необходимая нам при изучении греческой астрономии,- это теорема под номером III.1 на с. 194-197 немецкого перевода. Сопровождающий теорему чертеж дан на рис. II.7; арабские буквы, использованные на чертеже, заменены соответствующими буквами латинского алфавита.
Пусть у нас есть сфера с центром в точке Н. Нарисуем на ней дуги АВ и AG двух больших кругов; на этих дугах отметим произвольные точки D и Е, как показано на рисунке Затем проведем дуги DG и BE, пересекающиеся в точке Z. Прямые линии, которые мы видим на рисунке, для формулировки теоремы не нужны, они используются в доказательстве. Формулировка теоремы состоит из двух частей:
sin GE sin GZ sin BD
——— = ——— * ———
sin EA sin ZD sin ВA
sin GA sin GD sin BZ
——— = ——— * ———
sin AE sin DZ sin BE
Если я пишу, например, sin GE, то имею в виду синус угла, стягиваемого дугой GE. Птолемей приводит формулировку этой теоремы (только не для синусов, а для хорд) в главе 1.13 «Синтаксиса».
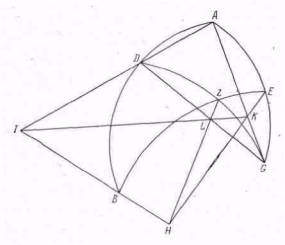Рис. II.7. Одна важная теорема из сферической тригонометрии AEG и ADB- дуги больших кругов на сфере, центром которой является точка Н Соединим точки D и G а также точки Е и В дугами больших кругов, и пусть дуги DG и BE пересекаются в точке ZТеорема связывает синусы дуг АВ, AG, BE, DG и различных дуг, на которые они разделены
Применяя данную теорему к прямоугольному сферическому треугольнику, изображенному на рис. II 6, мы получаем два важных соотношения.
sin a = sin A *sin с,
cos A = tg b/tg с. (II.11)
Если нам задан угол А и одна из сторон a, bили с, то из уравнений (II.11) мы можем найти две другие стороны Ясно, что для угла В выписываются уравнения, аналогичные уравнениям (II.11)
Птолемей уравнения (II.11) или их эквиваленты в терминах хорд не использует. Когда ему требуется соотношение, выраженное каким-либо из этих уравнений, он начинает с теоремы, стоящей у Менелая под номером III.1.
