ПРЕСТУПЛЕНИЕ КЛАВДИЯ ПТОЛЕМЕЯ

СОДЕРЖАНИЕ
Предисловие редактора перевода

Предисловие автора

Глава   I. Объяснение явлений в астрономии

Глава   II. Греческая математика

Глава   III. Земля

Глава   IV. Строение мира

Глава  V. Солнце и связанные с ним вопросы

Глава   VI. Долгота полной Луны

Глава   VII. Долгота Луны в любой фазе

Глава  VIII. Размеры Солнца и Луны. Расстояния до них

Глава   IX. Звезды

Глава   X. Движение Меркурия

Глава   XI. Венера и внешние планеты

Глава   XII. Некоторые второстепенные вопросы

Глава   XIII. Оценка деятельности Птолемея

Приложение А. Специальные термины и обозначения

Приложение Б. Метод Аристарха для нахождения размеров Солнца

Приложение В. Как Птолемей пользовался вавилонским календарем

Список литературы

2. Эпициклическая система

 

Самую большую трудность при изучении эпициклической системы представляет заучивание специальных терминов. Мы должны выучить их настолько хорошо, чтобы они стали для нас естественными и при­вычными. И тогда можно будет сказать, что эта система содержит лишь простые понятия и несложна для понимания.

Основные элементы данной системы, являющиеся по существу ге­ометрическими объектами, показаны на рис. IV.1. Эпициклическая система используется для описания движения тела на плоскости, и приступить к такому описанию мы должны с задания линии начала отсчета. На рисунке такой линией служит прямая Eі [1]). Наблюда­тель находится в точке Е. Круг, проходящий через точки A, В и G, называется кругом деферента, или просто деферентом; его центр на­ходится в точке Е. Греческие астрономы пользовались шестидесятеричными обозначениями и им было удобно считать радиус деферента BE равным 60. Мы в основном работаем в десятичной арифметике и поэтому берем радиус равным единице, если, конечно, мы не касаемся рассмотрения этой системы самими греками. Точка В равномерно движется по деференту в указанном направлении.

В систему входит еще один круг с центром в точке В. Точка Р - это небесное тело, чье положение мы хотим определить. В то время, когда точка В равномерно движется по деференту, точка Р равномерно движется по второму кругу, называемому эпициклом. Радиус эпицикла будем обозначать через r; r- это один из тех параметров, которые надо получить из наблюдений.

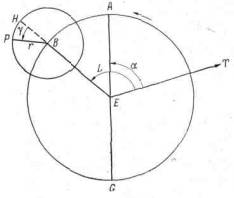
Рис. IV.1. Эпициклическая система (простейший случай). Наблюдатель на­ходится в точке Е, линия Eі - это линия начала отсчета, от нее измеря­ется угловое положение. Круг с цент­ром в точке E, проходящий через точ­ки А, В, G, называется деферентом. В большинстве случаев мы берем его ра­диус BEравным единице. Точка В дви­жется равномерно по деференту в на­правлении, указанном стрелкой. Точ­ка Р - небесное тело, положение ко­торого надо определить. В то время, когда точка В движется равномерно по деференту, точка Р движется равномер­но по кругу с центром в точке В. Этот круг радиуса РВ называется эпицик­лом. Линия ВН - продолжение ради­уса деферента BE. Эта дополнитель­ная прямая используется в рассужде­ниях

 

Если бы эпициклическую систему использовал какой-нибудь сов­ременный автор, то он, вероятно, измерял бы угловое положение радиуса РВ от некоторой фиксированной линии отсчета, например, от Eі или от ЕА. Греки же обычно измеряли положение этого радиуса по отношению к радиусу ВН, лежащему на продолжении радиуса де­ферента BE. Радиус ВН, очевидно, поворачивается с той же скоростью, с какой точка В движется по де­ференту. Радиус РВ может вра­щаться в любом направлении, и скорость его вращения - это еще один параметр, который на­до найти из наблюдений.

Угол BEіназывается сред­ней долготой точки Р, посколь­ку в среднем угловое положение точки В такое же, как и у точ­ки Р. Угол ВЕі будем обозна­чать буквой L. Эта угловая ве­личина является линейной функ­цией времени

L=L₀+n(t-t₀).       (IV.1)

Здесь t - время, t₀ - некото­рая удобная начальная эпоха, n называется средним движением (средняя угловая скорость), L₀ называется средней долготой в эпоху. Величины L₀ и n должны быть найдены из наблюдений.

Греки называли угол НВР, измеренный от НВ к РВ в на­правлении движения точки Р по эпициклу, аномалией. Мы будем обозначать аномалию буквой і. Аномалия также является ли­нейной функцией времени

і=і₀+і'(t-t₀)                 (IV.2)

Величинам і₀ и і' пока не будем давать никаких названий. Эти величины очевидно также являются параметрами, которые надо найти из наблюдений. Итак, всего из наблюдений мы должны определить значения пяти параметров. Это параметры L₀, n, і₀, і' и r [2]).

Греческие астрономы использовали эпициклическую систему двумя различными способами, которые, с современной точки зрения, выпол­няют две совершенно различные функции. В одном случае радиус эпицикла РВ всегда остается параллельным некоторой фиксированной прямой AGи на рисунке точка Р всегда находится, скажем, над точ­кой В. Очевидно, что в этом случае точка Р будет расположена дальше всего от точки Е, если точка В находится на деференте в точке А. Направление ЕА называется апогеем. Угол AEі, положительные значения которого соответствуют направлению против часовой стрелки, называется долготой апогея; обозначать ее мы будем буквой а. Точка Р расположена ближе всего к точке E, если точка В совпадает с точкой G на деференте, так что EG - это направление перигея.

Аномалия (угол РВН) возрастает в направлении, противополож­ном направлению движения точки В, а по размерам она равна углу BEА. Таким образом, мы можем отождествить угол BE А с аномалией і. Ясно, что

L=a+і                    (IV.3)

Здесь мы измеряем аномалию от апогея, как это было принято у греков. В современной астрономии ее чаще измеряют от перигея.

Теперь мы должны ввести еще несколько терминов. Угловое по­ложение точки Р по отношению к линии Еі будем называть дол­готой ». На рис. IV.1 это был бы угол PEі. Введем также величину е_с, которую назовем «уравнение центра». Такой термин появился в средневековье. Птолемей называет эту величину АБїГё±Ж±№БµГ№В. Переводчики Птолемея, работы которых я видел, этот термин вообще не переводят, а просто записывают его, используя буквы своего алфа­вита. Уравнение центра е_с - это разность между долготой » и сред­ней долготой L,

»=L+e_c.          (IV.4)

Используя тригонометрические функции угла на плоскости, найти значение е_с в эпициклической системе, которую мы сейчас рассматри­ваем, довольно просто:

e_c=arctg [-г sin і/(1+r cos і)].      (IV.5)

Чтобы полностью понять смысл этого выражения, разложим е_с в ряд по степеням r, отбросим все члены со степенями выше второй и приба­вим получившуюся сумму к L в уравнении (IV.4). Мы получим

»=L-r sin і+1/2 r² sin 2і,    (IV.6)

где углы измерены в радианах, а не в градусах [3]). Теперь орбита пла­неты вокруг Солнца с высокой степенью точности является эллипсом, в одном из фокусов которого расположено Солнце; такая орбита показана на рис. IV.2. Здесь S - это фокус эллипса APG, AG- боль­шая ось эллипса и Sі - направление начала отсчета. Точка G - это самая близкая S точка. Угол GSі обозначается Й и называется аргу­ментом перигелия [4]). Пусть расстояние CG равно единице. Расстояние CS назовем   эксцентриситетом   эллипса и обозначим через е. Угол PSі- это долгота »точки Р.

Воспользовавшись любым учебником по небесной механике, мы получим, что величину К можно записать в таком виде [5]):

»=M+Й+2e sin M+(5/4)e²sin 2M,                   (IV.7)

где М - определенная линейная функция времени [6]). Непосредствен­но сравнивать уравнения (IV.6) и (IV.7) мы не можем, поскольку в уравнение (IV.7) входит аномалия, измеренная от перигея, а анома­лия, входящая в уравнение   (IV.6),  измерена от апогея. Для того чтобы можно было сравнить эти уравнения, выпишем    соотношение     Й=А+а [7]). Тогда М+Й равно   М+А+а. С уче­том уравнения (IV.3) мы  теперь можем отождествить величину  М+А с аномалией і, которая также является линейной функцией   времени. Когда мы произведем   соответствующие  за­мены,   уравнение   (IV.7)   примет вид

»=L-2e sin і+ (5/4)е² sin 2і. (IV.8)

Если мы отождествим rв уравне­нии (IV.6) с 2е в уравнениях (IV.7) или (IV.8), то члены, пропорциональ­ные е, будут одинаковыми. Члены, пропорциональные е², отличаются на величину (3/4) е² sin 2і; максималь­ное значение этой величины равно (3/4)е². Для большинства объектов в Солнечной системе угол такого размера слишком мал, чтобы его можно было увидеть невооруженным глазом. Поэтому с той точ­ностью, которая была обычно доступна греческим астрономам, мы мо­жем сказать, что уравнение (IV.6) дает ту же самую долготу, что и эллипс.

Но эпициклическая модель не может согласовываться с эллипти­ческой и по долготе, и по расстоянию. На рис. IV.1 хорошо видно, что в эпициклической модели расстояние до точки Р изменяется от (1-r) до (1+r); в случае эллиптической орбиты (рис. IV.2) это рас­стояние изменяется от (1-е) до (1+е). Если мы считаем равными вели­чины r и 2е, то эпицикл дает вдвое большее изменение расстояния, чем эллипс. Если же мы приравниваем изменения расстояния, т. е. равны­ми считаем величины rи е, то эпицикл дает только половину правильно­го изменения долготы.

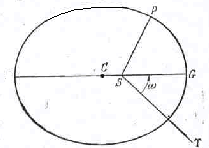
Рис. IV.2. Эллиптическая орбита. Точка S - центр гравитации, на­ходится в одном из фокусов эллип­са. Точка G - это ближайшая к S точка орбиты. Sі - направление начала отсчета. Угол GSі, обозна­ченный Й,- долгота перигея (или перигелия). Угол PSі -долгота точки Р. Если расстояние СS взя­то равным единице, то расстояние CS равно эксцентриситету эллипса.

 

 

Некоторые авторы, в том числе и я, говорили, что греческие аст­рономы не могли изучать расстояния до небесных тел с необходимой точностью, и поэтому они не понимали основного недостатка своей главной геометрической модели. Это утверждение о расстоянии верно, если рассматривать Солнце. Однако в процессе работы над этой книгой я понял, что его нельзя отнести к Луне и планетам. Как мы увидим в следующих главах, греческие астрономы могли точно измерять изме­нение расстояния до планеты, хотя и не могли измерять среднее расстояние до нее. Для Луны же они могли точно находить и среднее рас­стояние, и его изменение. Таким образом, у греческих астрономов была информация, необходимая для установления того, что эпицикличе­ская модель в корне ошибочна и для Луны, и для планет.

Эллиптическая модель и некоторые другие дают возможность пра­вильно вычислять одновременно изменение и расстояния, и долготы. У греческих астрономов была одна такая модель (я дам ее описание в разделе IV.5), и они применяли ее ко всем планетам кроме Меркурия. Странно, что они никогда не применяли эту модель для описания движения Луны, которое они знали лучше всего.

В конце раздела IV.1 я использовал понятие эпициклической систе­мы для обозначения всего комплекса систем; эти системы могут вклю­чать кроме эпицикла и деферента и другие элементы. Если привести все эти системы сразу в одной главе, то читатель будет просто пере­гружен информацией, и я, конечно, этого не сделаю. Однако два услож­нения той простой системы, которую мы сейчас описали, лучше при­вести именно здесь. Ведь мы не сможем даже начать детальное изучение греческой астрономии, если не разберемся в первом из этих усложне­ний; второе же мы должны понять прежде, чем рассматривать учение греков о планетах. Первым усложнением я займусь даже раньше, чем приведу второй из тех способов применения эпициклической модели (рис. IV.1), какими пользовались греческие астрономы.

 

---