6. Модель, которую греки никогда не использовали
На рис. IV.5 показана одна из модификаций модели экванта (см. рис. IV.4). На мой взгляд, эта модификация очевидная, но насколько я знаю, греческие астрономы никогда не пробовали представить движение такой моделью. Рис. IV.5 отличается от рис. IV.4 только тем, что на нем есть второй дополнительный эпицикл. Соответствующую модель можно назвать моделью вторичного эпицикла. В такой модели точка Р больше не находится на круге с центром в точке В. Вместо нее по этому кругу с центром в точке В равномерно движется точка С. Планета Р равномерно движется по второму эпициклу с центром в точке С. Конечно, не обязательно добавлять второй эпицикл именно к модели экванта. Этот второй круг вполне можно было добавить, например, к модели, изображенной на рис. IV.1.
Греческие астрономы такой моделью никогда не пользовались, по крайней мере она не упоминается ни в одной из известных нам работ. Астрономы стран ислама ввели второй эпицикл около 1300 или 1350 г., использовал его также и Коперник [Коперник, 1543, глава IV.3]. Неизвестно, ввел ли Коперник вторичный эпицикл независимо, или же он знал, что до него вторичный эпицикл рассматривали мусульманские астрономы
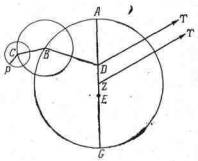
Рис. IV.5. Модель вторичного эпицикла. К модели, изображенной на рис. IV.4, добавим еще один эпицикл. Теперь по кругу с центром в точке Z равномерно движется не планета Р, а точка С. Планета Р движется равномерно по другому кругу с центром в точке С. Греки такой моделью никогда не пользовались, хотя у них были модели и посложнее. В средние века рассматривались модели, похожие на эту.
Хотя греческие астрономы и не использовали второй эпицикл, модель вторичного эпицикла и проще, и точнее некоторых их моделей. Это замечание особенно важно по отношению к моделям, которые Птолемей использовал для Луны и Меркурия (они будут рассмотрены в разделах VII.3 и Х.1). Более того, эту модель можно использовать для всех планет и не вводить для Меркурия отдельную модель.
Модель может показаться очевидной, поскольку наше представление о движении планеты определяется идеей эллиптической гелиоцентрической орбиты. С этой точки зрения нам довольно просто дать интерпретацию различных элементов модели, изображенной на рис. IV.5. Точка В представляет Солнце. Деферент - это геоцентрическая орбита Солнца, если мы рассматриваем Меркурий или Венеру, и это планетоцентрическая орбита Солнца, если имеем дело с внешней планетой. Использование двух эксцентриситетов DZ и ZE позволяет нам с хорошей точностью описать орбиту Солнца. Точка Р должна двигаться вокруг точки В по эллиптической орбите, и использование вторичного эпицикла дает нам вполне приемлемую аппроксимацию такой орбиты.
Ясно, что направление радиуса СР должно совпадать с тем направлением, в каком с Солнца виден соответствующий афелий. Мы уже знаем, что эпицикл не может одновременно представлять и долготу, и радиальное расстояние на эллиптической орбите с хорошей точностью. Поскольку мы «смотрим» на радиус СР из точки Е, то нас интересует и радиальное расстояние от точки В до точки Р, и угловое положение точки Р, какое получается, если смотреть из точки В. Эго означает, что длина радиуса СР должна давать нам разумный компромисс между тем, с какой точностью мы получаем угол, и тем, с какой точностью мы получаем расстояние. Поэтому длина СР, наилучшим образом удовлетворяющая данным, лежит, вероятно, между значением эксцентриситета гелиоцентрической орбиты (в современном понимании этого термина) и удвоенным его значением.