Г л а в а X
ДВИЖЕНИЕ МЕРКУРИЯ
1. Модель Птолемея для орбиты Меркурия
Для Венеры и внешних планет Птолемей пользуется моделью экванта (см. раздел IV.5). В разделе IV.5 были изложены причины, по которым для Меркурия эта модель не может хорошо «работать». Более детально ситуация показана на рис. Х.1. Этот рисунок повторяет рис. XIII.9 из АРО.
На рисунке изображены гелиоцентрические орбиты Меркурия и Земли, масштаб примерно выдержан. Для рисунка использованы значения параметров, соответствующие времени Птолемея. Направление от Солнца на ОЕ указывает на перигелий орбиты Земли, а направление на О@ указывает на перигелий Меркурия. Отрезок GSA - это большая ось орбиты Меркурия. Точка @1 - афелий этой орбиты, а точка @2 - перигелий. Прямая Sі указывает на точку весеннего равноденствия. Угол ОЕ Sіпримерно равен 71,04°, а угол О@ Sі примерно равен 48,39°.
Когда Птолемей строил свою теорию Меркурия, основными данными, с которыми он работал, были измерения максимальной элонгации. Предположим, например, что Земля находится в точке Е, а Меркурий находится в произвольной точке своей орбиты. Проведем из точки Е прямые, касательные к орбите Меркурия. Если с Земли Меркурий виден слева от точки S и если Меркурий находится в одной из точек касания, то такое положение соответствует наибольшему возможному удалению планеты на восток для данного положения Земли. Если Меркурий находится в другой точке касания, то из точки Е (положение Земли) Меркурий виден в наибольшем удалении на запад от Солнца.
Пусть теперь »@ - это геоцентрическая долгота Меркурия, когда он находится в одной из точек касания, a LQ - геоцентрическая долгота среднего Солнца в этот момент времени. Обозначать наибольшую элонгацию я буду символом D@, а определять ее буду так [1]):
D@= »@ - LQ. (X.1)
Если D@ положительна, то Меркурий находится к востоку от Солнца. В этом случае он будет вечерней звездой. Если D@ отрицательна, то Меркурий - утренняя звезда, находящаяся к западу от Солнца.
Величина D@ является функцией величины LQ. График этой функции изображен на рис. Х.2. Наибольшая восточная (+) элонгация показана в верхней части рисунка, а наибольшая западная (-) элонгация показана в нижней части. Пронумерованными точками отмечены наблюдения, которые Птолемей использует для нахождения параметров орбиты Меркурия; мы их рассмотрим несколько позже. При построении кривых на рис. Х.2 использованы те же значения параметров, что и для построения рис. Х.1, т. е. рис. Х.2 также соответствует эпохе Птолемея.
Когда Меркурий был виден к востоку от Солнца, то наибольшее расстояние от Солнца до него было примерно равно 26° 16'. Долгота LQ в этот момент составляла около 100°. Наименьшее положительное значение D@ было примерно равно 19°23'. Такое расстояние соответствовало значению LQ, равному примерно 274°. В то же время наибольшее по абсолютной величине отрицательное значение -25°47' соответствовало значению LQ, примерно равному 339°, а наименьшее по абсолютной величине отрицательное значение -19°50' соответствовало средней долготе Солнца LQ, примерно равной 145° [2]). У этих чисел есть два интересных свойства. Во-первых, значения LQ для наибольшего «восточного» и наибольшего «западного» значений D@ отличаются примерно на 120°, точно так же, как и значения LQ, соответствующие самому маленькому «восточному» и самому маленькому «западному» значениям. Во-вторых, разница между модулями наибольших «западного» и «восточного» значений, так же как и разность модулей наименьших значений, примерно равна 0,5°. Мы должны спросить, а что случилось бы, если бы гелиоцентрическая орбита Меркурия была кругом. Напомним, что у Венеры орбита почти
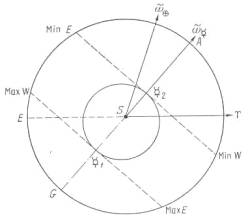Рис. Х.1. Гелиоцентрические орбиты Меркурия и Земли. Масштаб для орбит примерно выдержан. Использованные орбитальные параметры соответствуют эпохе Птолемея. Прямая от S к і направлена на точку весеннего равноденствия, прямая, идущая к О@, направлена на перигелий Меркурия, а прямая, идущая к ОЕ на перигелий Земли. Точка @1 - это афелий Меркурия, точка @2 - его перигелий. Штриховые линии касаются орбиты Меркурия в точках афелия и перигелия. Смысл обозначений Мах Е, Min W и других объяснен в тексте. Этот рисунок повторяет рис. XIII.9 из АРО
круговая. Как мы увидим в разделе XI.3, первое свойство для Венеры и для Меркурия почти идентично, а вот о втором свойстве этого не скажешь. У Венеры разница между соответствующими «восточным» и «западным» значениями не 0,5°, а 0,2°. Таким образом, наиболее очевидная проблема, стоящая для Меркурия,- это отсутствие симметрии в направлении восток - запад. Но в большей части материала, посвященного рассмотрению данного вопроса, который я читал, доказывается, по-видимому, что такой проблемой является разница между значениями LQ, хотя на самом деле эта задача одинакова и для Меркурия, и для Венеры [3]).
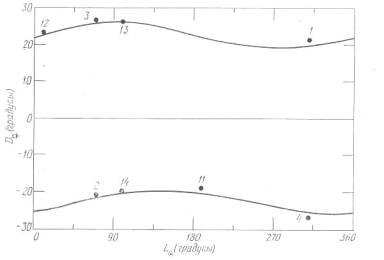Рис. Х.2. Наибольшая элонгация Меркурия как функция средней долготы Солнца LQ; LQсоответствует геоцентрическому положению Солнца. Верхняя кривая (наибольшая элонгация D@положительная) соответствует восточным элонгациям, когда Меркурий является «вечерней звездой», а нижняя кривая соответствует западным элонгациям, когда Меркурий - «утренняя звезда». Кривые вычерчивались по значениям параметров на время Птолемея. Пронумерованными точками обозначены наблюдения, которыми Птолемей пользуется при построении своей теории Меркурия
Данная задача очень похожа на «задачу об эвекции Луны». Величина D@ для Меркурия играет роль, аналогичную Е - максимальному значению уравнения центра для Луны. В обоих случаях Е или его аналог D@ сильно изменяется в зависимости от положения на орбите. А это значит, что вместе со средней долготой должен меняться либо радиус эпицикла, либо радиус деферента.
Птолемей утверждает, что для Луны он задачу решил с помощью «кривошипно-шатунной» модели, изображенной на рис. VII.2. Серьезные недостатки этой модели не остановили Птолемея, и он использует аналогичную идею для Меркурия. То есть, выбирая между возможностью изменять либо r (радиус эпицикла), либо R (радиус деферента) [4]), Птолемей снова изменяет R.
Модель Птолемея для Меркурия показана на рис. Х.З. Как обычно, буквой Е обозначена Земля, Y - это точка весеннего равноденствия. Направление прямой от точки Е то точки А Птолемей называет апогеем. На самом деле это апогей деферента, а не самого Меркурия, но Птолемей, говоря о планете, обычно так понимает апогей. Угол от Eі до ЕА называется долготой а апогея Меркурия.
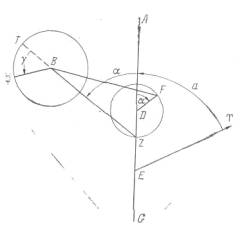
Рис. Х.З. Модель Птолемея для Меркурия. Точка В - центр эпицикла Меркурия, @ - положение Меркурия. Точка Е - Земля, прямая Eі направлена на точку весеннего равноденствия. Точку А Птолемей называет апогеем, но это скорее апогей деферента, чем самой планеты. Долгота а апогея - это угол от Eі до ЕА, измеренный в указанном направлении. Точка Z находится между Е и А, и центр эпицикла- точка В - равномерно вращается в указанном направлении вокруг Z, а не вокруг Е. Точка D находится между точками Z и А, точка F вращается вокруг D в указанном направлении. Точка F вращается стой же скоростью, что и В, так что угол ADF всегда равен углу ± между ZA и ZB. В процессе движения постоянным остается расстояние BF, а не расстояние BZ. Аномалия іпланеты возрастает в указанном направлении. Она измеряется от точки Т, лежащей на продолжении линии ZB
На небольшом расстоянии от точки Е в направлении точки А лежит точка Z. Расстояние EZ я буду называть «первый эксцентриситет» и обозначать е1. Точка В лежит на деференте, и прямая BZ равномерно вращается вокруг Z. Короткого названия для угла а между ZA и ZB нет; я буду называть его «среднее расстояние до апогея Меркурия». Угол а возрастает в указанном направлении. Точка Dнаходится на небольшом расстоянии е2 от точки Z в направлении к точке А; расстояние е2 я буду называть «второй эксцентриситет». Точка В вращается вокруг Z; точка F вращается вокруг точки D с той же самой скоростью, но в противоположном направлении, поэтому угол ADF также равен ±. Во время движения постоянным остается расстояние BF, а не расстояние BZ. Радиус DF назовем «третьим эксцентриситетом» е3. Наконец, @ - это положение Меркурия. Аномалия і измеряется от точки Т, лежащей на продолжении линии ZB.
Сумма углов а и ± равна средней долготе Солнца LQ.
LQ = a + ±. (X.2)
Птолемей использует это соотношение в явном виде при построении теории Меркурия.
Если ±=0, то Точка Fнаходится прямо над точкой D, а точка В - над точкой F. В этом случае расстояние от Е до В равно постоянному расстоянию BF плюс сумма трех эксцентриситетов. Это наибольшее возможное расстояние между точками В и Е. Если ± =90°, то расстояние от точки В до точки D минимальное, а вот расстояние от точки В до точки Е продолжает еще некоторое время уменьшаться с возрастанием ±. Точка В ближе всего к Е, если угол а равен примерно 120°. Поскольку картина симметрична относительно прямой ЕА, то точка В находится на таком же расстоянии от точки Е, если угол а примерно равен 240°. Описывая данную ситуацию, Птолемей говорит, что Меркурий проходит перигей дважды за каждое обращение [глава IX.8]. Имеет же он в виду то, что для центра эпицикла в течение каждого земного года существует два положения перигея. Сама планета за каждое полное обращение точки @ вокруг точки В (примерно за 116 суток) [5]) проходит через перигей один раз. Другими словами, Меркурий находится в перигее, если значение у близко к 180°. Следующий раз он будет в перигее, когда у близка к 180°+ 360°. Значение gувеличивается на 360° примерно за 116 суток.
Аномалия g является линейной возрастающей функцией времени. Обозначим через g@0 значение g в некоторую эпоху, например, в фундаментальную эпоху Птолемея [6]), а через g@ обозначим изменение у за одни сутки. Тогда g@0 и g@ - параметры, которые надо определить из наблюдений. Положение апогея а, три эксцентриситета е1, е2 и е3, радиус эпицикла r также должны быть найдены из наблюдений. Кроме того, Птолемей предполагает, что значение а может изменяться со временем, т. е. скорость аў такого изменения - еще один параметр, который нужно определить. Всего Птолемею из анализа наблюдений надо было найти восемь параметров.
