ПРЕСТУПЛЕНИЕ КЛАВДИЯ ПТОЛЕМЕЯ

СОДЕРЖАНИЕ
Предисловие редактора перевода

Предисловие автора

Глава   I. Объяснение явлений в астрономии

Глава   II. Греческая математика

Глава   III. Земля

Глава   IV. Строение мира

Глава  V. Солнце и связанные с ним вопросы

Глава   VI. Долгота полной Луны

Глава   VII. Долгота Луны в любой фазе

Глава  VIII. Размеры Солнца и Луны. Расстояния до них

Глава   IX. Звезды

Глава   X. Движение Меркурия

Глава   XI. Венера и внешние планеты

Глава   XII. Некоторые второстепенные вопросы

Глава   XIII. Оценка деятельности Птолемея

Приложение А. Специальные термины и обозначения

Приложение Б. Метод Аристарха для нахождения размеров Солнца

Приложение В. Как Птолемей пользовался вавилонским календарем

Список литературы

4. Точность птолемеевой модели Меркурия

 

В разделе XIII.8 АРО я составил две вычислительные программы. Одна вычисляла геоцентрическую долготу Меркурия по теории Птолемея, а другая - по теориям Ньюкома для Меркурия и для Солнца [Ньюком, 1895а и 1895]. По этим программам было получено значение долготы на 51 момент времени с промежутком в 80 суток. В качестве среднего момента в этих расчетах я взял полдень 20 июля 137 г. У Птолемея часто можно встретить такую эпоху, и она соответствует середине его астрономической деятельности. К птолемеевой долготе апогея я прибавил 1,1°, поскольку все долготы у Птолемея примерно на такую величину меньше, чем нужно. С достаточной степенью точности можно считать, что за весь промежуток в 4000 дней и Меркурий, и Земля, сделали целое число обращений вокруг Солнца.

Наибольшая погрешность, полученная при сравнении выборки из 51 значения, полученного по теории Птолемея, со значениями, полученными по теориям Ньюкома, равна 7,84°. Такая погрешность соответствует центральной дате, использованной для сравнения, 20 июля 137 г. Среднее квадратичное отклонение погрешности составило 2,99°.

В разделе VII.8 я уже упоминал высказывание Дрейера о том, что теории Птолемея настолько точно представляют движения в солнечной системе, насколько наблюдатель (времен древних греков) мог следить за ними [Дрейер, 1905, с. 200]. Мне трудно поверить, что Дрейер изучал точность моделей Птолемея. Как мы видели, утверждение Дрейера не подходит ни для Солнца, ни для Луны. Теперь мы видим, что погрешности птолемеевой модели Меркурия можно характеризовать только как большие. Среднее квадратичное отклонение координат в звездном каталоге, например, составляет всего лишь около 20' по каждой координате (раздел IX.2). Это можно принять за точность, с какой греческие наблюдатели могли следить за планетами. Среднее квадратичное отклонение в модели Птолемея для Меркурия почти точно равно 3°, т. е. почти в десять раз превышает точность наблюдений.

Затем я начал изменять параметры в модели Птолемея до тех пор, пока не нашел значения, сводящие к минимуму среднее квадратичное отклонение. Результаты такого исследования собраны в таблице Х.2 [1]). В первом столбце этой таблицы назван параметр, второй столбец дает значение этого параметра, найденное Птолемеем. Здесь я сделал два отступления от практики Птолемея при рассмотрении движения Меркурия.

 

 

Таблица Х.2

Сравнение птолемеевых параметров для Меркурия с «наиболее подходящими» значениями

 

 

Длина «шатуна» BF (рис. Х.З) кажется мне более фундаментальным свойством модели, чем расстояние АЕ. Поэтому, вместо того чтобы соотносить все расстояния расстоянию АЕ, я соотношу их длине r «шатуна» BF и считаю длину r равной не 120, а 1. Это близко ко второму нормированию, проведенному Птолемеем.

В третьем столбце таблицы Х.2 даны значения параметров, приводящие к наилучшему сточки зрения точности варианту данной модели. При использовании этих значений наибольшая погрешность падает с 7,84° до 3,26°, а среднее квадратичное отклонение уменьшается с 2,99° до 1,70°. Но даже с «самыми подходящими» значениями параметров модель и близко не подходит к такому описанию движения Меркурия, которое не уступало бы той точности, с какой греческие наблюдатели могли следить за его движением.

Новые значения параметров также представляют интерес. Например, значение долготы апогея почти на 30° больше значения, найденного Птолемеем. В этом случае из-за большой эксцентричности орбиты Меркурия (рис. Х.1) определить апогей Меркурия проще, чем найти апогей почти круговой орбиты Венеры. И все же, как мы увидим в разделе XI.4, Птолемей определяет долготу апогея Венеры с ошибкой лишь в 4°, в то время как ошибка при определении положения апогея Меркурия составляет почти 30°. Надо выяснить происхождение этой аномально большой ошибки, но я отложу это до раздела Х.5.

Следует отметить, однако, что с точки зрения точности его модели ошибка в положении апогея не является самой серьезной. Я постарался узнать, что же получится, если менять только значение долготы апогея, а всем остальным параметрам оставить значения, найденные Птолемеем. В этом случае наилучшая точность достигается при значении долготы апогея, равном 219,6° (почти такое значение и стоит в таблице Х.2). Среднее квадратичное отклонение получается равным 2,54°. Так что даже «самое подходящее» значение положения апогея не сильно увеличит точность модели, если не менять остальные параметры.

«Наиболее подходящие» значения радиуса эпицикла, аномалии в эпоху 20 июля 137 г. и скорости изменения аномалии близки к значениям Птолемея. Самые большие погрешности получаются, если использовать найденные Птолемеем значения для трех эксцентриситетов. Значения трех эксцентриситетов даже приблизительно нельзя считать равными. «Наиболее подходящее» значение e₁ намного больше, чем значение этого параметра у Птолемея, а значения e₂ и e₃ намного меньше. Более того, «наиболее подходящее» значение для e₂ отрицательно. А это значит, что на соответствующей модели (рис. Х.3) точка D должна быть не выше точки Z, а ниже этой точки.

«Наиболее подходящие» значения e₂ и e₃ очень маленькие. Поэтому я и попробовал, что получится, если все остальные параметры взять из третьего столбца таблицы Х.2, а эти два параметра положить равными нулю. В этом случае среднее квадратичное отклонение возросло с 1,70° лишь до 1,73°; незначительное изменение.

Таким образом, вместо своей модели Птолемей должен был использовать простую модель, изображенную на рис. Х.8. Эта модель соответствует тому случаю, когда мы считаем параметры e₂ и e₃ равными нулю. Круг, по которому на рис. Х.3 движется точка F, сжался в точку D, а сама точка Dсовпадает теперь с точкой Z. Вот мы и получили простую модель эксцентра, которая описывает движение центра эпицикла, точки В.

Интересно отметить, что модель на рис. Х.8 все еще сохраняет одно важное свойство, которое Птолемей хотел описать своей моделью. Это существование пар значений L_Q, которым соответствуют наибольшие и наименьшие значения D_@. Эти пары значений показаны на рис. Х.2. Как видно из этого рисунка, в эпоху Птолемея наибольшая восточная элонгация D_@ соответствовала L_Q= 100°, а наибольшая западная элонгация соответствовала L_Q=339°. To же самое мы видим и для

 

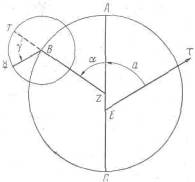
Рис. Х.8. Модель движения Меркурия. Птолемею надо было использовать эту модель. Если рассмотреть все модели, которые можно получить из «кривошипно-шатунной» (рис. Х.З), то точность данной модели будет почти наилучшей из возможных. Заметим, что «кривошип» на рис. Х.З теперь сжался в одну точку. Другими словами, «кривошипно-шатунная» модель не увеличивает точность. Наоборот, она мешает получить хорошую точность

 

наименьших значений: наименьшая восточная элонгация в эпоху Птолемея была при L_Q=274°, а наименьшая западная - при L_Q=145°. На рис. Х.9 показано, какие значения D_@ получаются в простой модели, изображенной на рис. Х.8. Для этой модели все параметры, кроме е₂ и е₃, взяты из таблицы Х.2, a e₂=e₃=0. На рис. Х.2 и Х.9 наибольшим и наименьшим значениям D_@ соответствуют примерно одинаковые значения L_Q, но общее колебание значений D_@ на рис. Х.9

 

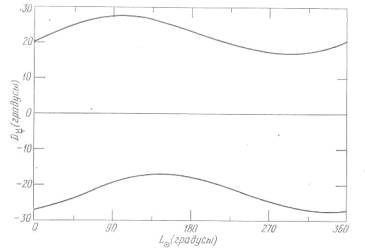Рис. Х.9. Наибольшая элонгация Меркурия D_@ как функция средней долготы Солнца L_Q. Зависимость определяется моделью, изображенной на рис. Х.8. Рис. Х.9 хорошо согласуется с зависимостью, показанной на рис. Х.2. Напомним, что рис. Х.2 получен с помощью значений, вычисленных по современной теории. Основным моментом является то, что «кривошипно-шатунный механизм» из модели Птолемея вовсе не нужен для описания самого удивительного свойства движения Меркурия. Наличие двух максимумов и двух минимумов порождается эксцентром, а не «кривошипом»

 

больше. Это значит, что при условии е₂=е₃=0 «наилучшее значение» для ег несколько меньше, чем значение в таблице Х.2. Не следует удивляться тому, что нужно немного изменить значение е₁. Ведь при составлении таблицы Х.2 наложенные здесь ограничения (е₂=е₃=0) не рассматривались.

Самой характерной чертой модели Птолемея является «кривошипно-шатунный механизм». Однако, как показывает рис. Х.9, вовсе не этот механизм служит причиной существования пары наибольших и пары наименьших значений D_@; этот механизм к данному явлению отношения не имеет. Существование пар экстремальных значений обусловлено эксцентром, поэтому мы получим пары значений даже в том случае, если совсем откажемся от «кривошипа».

В эпоху Птолемея не было математической теории, необходимой для составления таблицы Х.2. И если мы хотим заниматься непосредственно работой Птолемея, а не установлением степени точности его теории, мы должны сравнить его модель с тем, что он мог бы получить на основе имевшихся в то время знаний. Другими словами, вместо нахождения параметров современными статистическими методами мы должны найти их методами, доступными Птолемею. Для этого мы должны по методике Птолемея найти параметры a, е₁ ,е₂, е₃ и r из данных, использовавшихся для установления зависимости, изображенной на рис. Х.2.

Таблица   Х.З

Некоторые наибольшие элонгации Меркурия

LQ, градусы	D@, градусы	LQ, градусы	D@, градусы
100	максимальное      «восточное» значение	40 220	+24,277 -21,327
340	максимальное «западное» значение	130 130	+25,562 - 19,914

Набор значений, внесенных в таблицу Х.3, аналогичен тому множеству значений, которым пользовался Птолемей. Однако они взяты из значений, использовавшихся при построении графика на рис. Х.2. В таблице я сделаю небольшое упрощение, и теперь наибольшее «восточное» значение соответствует L_Q=100°, а наибольшее «западное» значение соответствует L_Q=340°. Эти данные нужны только для определения положения апогея, и незначительное их изменение окажет практически ничтожное воздействие на результаты. Если взять такие значения, то долгота апогея равна 220°. Определив положение апогея в свою эпоху, Птолемей по «западному» (отрицательному) значению в апогее (220°) и «восточному» (положительному) значению в диаметрально противоположной точке (40°) находит значения r и е₂₊е₃. Полученные Птолемеем значения этих величин даны в уравнениях (Х.3) и (Х.4). Затем он берет и «восточное», и «западное» значения в точке, отстоящей от положения апогея на 90°, т. е. в точке 130°, и по этим значениям находит е₂ и е₃. Теперь по известным значениям e₁ и е₂+е₃ он находит значение е₂.

Результаты применения метода Птолемея к данным из таблицы Х.3 показаны в таблице Х.4. Их нужно сравнить с «наиболее подходящими» значениями параметров из последнего столбца в таблице Х.2. Значения r и долготы апогея очень близки. А вот значение е₁ получилось близким к значению, найденному Птолемеем. Но самое интересное в том, что е₂ и е₃ снова очень маленькие, как и в последнем столбце таблицы Х.2. Другими словами, метод Птолемея, примененный к точным данным, также приводит

 

Таблица   Х.4

Параметры, полученные по данным из таблицы Х.3

 

нас к простой модели, изображенной на рис. Х.8, а не к сложной «кривошипно-шатунной» модели, показаной на рис. Х.3.

Теперь мы должны привести ту непосредственную причину, которой Птолемей обосновывает необходимость введения «кривошипно-шатуного» механизма. В главе IX.8 «Синтаксиса» он отмечает, что при L_Q, равной 10°, значение D_@ равно 23 1/4 градуса. Но тогда центр эпицикла находится в точке С (рис. Х.5). А в этом случае и восточная, и западная элонгации имеют одно и то же значение. Поэтому сумма двух элонгации в этом положении равна 46 1/2 градуса. Когда L_Q равна либо 70°, либо 310°, то по данным из таблицы Х.1 сумма двух элонгации равна 47 3/4 градуса, т. е. больше, чем при L_Q, равной 10°.

Рис. Х.6 показывает, что сумма двух элонгации - это тот угол, под которым из точки Е (положение Земли) «виден» эпицикл. А. поскольку при L_Q 70° или 310° этот угол больше, чем при L_Q 10°> то по Птолемею центр эпицикла при L_Q=70° или 310° должен быть ближе к Земле. Именно это явление и привносит Птолемей в свою модель введением «кривошипно-шатунного» механизма.

Но Птолемей ошибается. Если L_Q равна 40° (а именно такое значение соответствует действительному положению точки G на рис. Х.5), то положительная (восточная) элонгация равна 24,277°. Поскольку ситуация не абсолютно симметричная, то западная элонгация немного

 

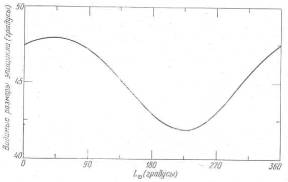Рис. Х.10. «Видимые» размеры эпицикла Меркурия как функция средней долготы Солнца L_Q. График построен по значениям параметров, соответствующим эпохе Птолемея. Если деферент ближе всего к Земле (перигей), то видимые размеры самые ' большие, а если деферент дальше всего от Земли (апогей), то видимые размеры самые маленькие. Вопреки утверждению Птолемея, имеется только одно положение перигея

 

 

меньше и сумма двух элонгации равна 47,926°. В точке, отстоящей от этой точки на 60° (L_Q равна 100°), сумма двух элонгации составляет всего лишь 46,788°, и почти такая же сумма получается при L_Q=340°. Итак, деферент в точке G ближе к Земле, чем в точках, отстоящих от точки G на 60°, точно так же как и для простой модели, изображенной на рис. Х.8.

В точке Gдеферент ближе к Земле, чем в какой-либо другой точке. Это можно увидеть с помощью рис. Х.10. Я вычислил сумму наибольшей восточной элонгации и наибольшей западной элонгации и изобразил на рис. Х.10 эту сумму как функцию величины L_Q. Сумма двух элонгации равна углу, под которым из точки Е «виден» эпицикл. На рисунке этот угол назван «видимыми размерами эпицикла». Хорошо видно, что функция имеет единственный минимум около точки L_Q =220°. У Птолемея здесь должен быть апогей, т. е. в этой точке деферент дальше всего от Земли. Максимум у кривой также единственный около L_Q=40°. У Птолемея здесь должен быть перигей, т. е. эта точка деферента ближе всего к Земле.

Мы получили, что имеются единственное положение перигея и единственное положение апогея, вопреки утверждениям Птолемея. И снова мы не находим никакого оправдания «кривошипно-шатунному» механизму, введенному Птолемеем.

С какого бы места мы ни начали свои рассуждения, мы не можем найти обоснование «кривошипно-шатунной» модели. Точных результатов эта модель не дает, не нужна она и для того, чтобы получить пары максимальных и минимальных значений D_@. Анализ данных, проведенный с достаточной точностью, не приводит к подобной модели. И наконец, вопреки действительности, в этой модели получаются два положения перигея. Я могу найти лишь одно объяснение создавшемуся положению дел: Птолемей не разобрался в ситуации; я покажу это в следующем разделе.

---