ПРЕСТУПЛЕНИЕ КЛАВДИЯ ПТОЛЕМЕЯ

СОДЕРЖАНИЕ
Предисловие редактора перевода

Предисловие автора

Глава   I. Объяснение явлений в астрономии

Глава   II. Греческая математика

Глава   III. Земля

Глава   IV. Строение мира

Глава  V. Солнце и связанные с ним вопросы

Глава   VI. Долгота полной Луны

Глава   VII. Долгота Луны в любой фазе

Глава  VIII. Размеры Солнца и Луны. Расстояния до них

Глава   IX. Звезды

Глава   X. Движение Меркурия

Глава   XI. Венера и внешние планеты

Глава   XII. Некоторые второстепенные вопросы

Глава   XIII. Оценка деятельности Птолемея

Приложение А. Специальные термины и обозначения

Приложение Б. Метод Аристарха для нахождения размеров Солнца

Приложение В. Как Птолемей пользовался вавилонским календарем

Список литературы

3. Птолемеевы параметры для орбиты Меркурия

Как мы видели в разделе Х.1, модель Птолемея для Меркурия имеет восемь параметров. Определить их надо из наблюдений. Для нахождения этих параметров Птолемей использует в общей сложности 17 наблюдений. Одно из них - это наблюдение соединения Меркурия с Луной, рассмотренное в предыдущем разделе. Птолемей использует его пятнадцатым по счету. Наблюдение было проведено, когда Меркурий был виден к востоку от Солнца, но не достиг наибольшей элонгации. Последними из семнадцати наблюдений Птолемей использует два наблюдения, проведенные с промежутком в 4 дня в -264 г. Меркурий был виден к востоку от Солнца, но еще не на максимальном удалении. Все четырнадцать первых наблюдений были проведены, когда элонгация Меркурия была наибольшей, для семи из них Меркурий был виден к востоку от Солнца и для семи - к западу.

Начну я с рассмотрения наблюдений наибольшей элонгации. Мне кажется, приводить записи этих наблюдений из текста Птолемея не обязательно. Первые десять наблюдений можно найти в главе IX.7 «Синтаксиса», два следующие в главе IX.8 и описание двух оставшихся наблюдений есть в главе IX.9. В некоторых записях прямо дана разница по долготе между Меркурием и определенной звездой. В других записях описана конфигурация Меркурия и двух или большего числа звезд. Такие описания достаточно детальны. По ним можно определить долготу Меркурия, если положения звезд взять из звездного каталога. Эти записи подробно рассмотрены в АРО [с. 182-190].

Данные из записей собраны в таблице Х.1. В первом столбце стоит порядковый номер наблюдения, которым мы будем пользоваться в дальнейшем обсуждении. В следующий столбец помещена дата наблюдения, а в третьем столбце назван наблюдатель. В четвертом столбце стоят значения средних долгот Солнца, а в пятом - элонгации D_@ Меркурия. Элонгация D_@ определяется из уравнения (Х.1). В это уравнение входит средняя, а не истинная долгота Солнца. Значения, стоящие в этих столбцах, взяты из записей Птолемея. Если читателю потребуется измеренная долгота Меркурия, то он может найти ее по значениям L_Q и элонгации.

Элонгацию, приведенную Птолемеем, можно сравнить с вычисленной по современной теории. В такое сравнение войдет и погрешность в птолемеевых солнечных таблицах, и погрешность при измерении долготы Меркурия, поэтому более поучительно рассмотреть погрешность в измеренной долготе, а не в элонгации Меркурия. Такая погрешность и дана в последнем столбце таблицы.

Нужно сделать несколько замечаний. Восемь наблюдений были проведены в эпоху Птолемея: семь - якобы им самим, и одно,- его современником Теоном. Шесть наблюдений были проведены между 12 февраля -261 г. и 30 октября -236 г.

 

 

 

 

Таблица   X.I

Наблюдения Меркурия в наибольшей элонгации

 

Четыре из этих наблюдений принадлежат Дионисию. О Дионисии мы ничего не знаем кроме того, что он провел эти и некоторые другие наблюдения. Еще для двух наблюдений, также древних для Птолемея, наблюдатель не назван. Основываясь на хронологии, можно предположить, что их проделал Дионисий, но стиль записей и единицы измерения делают такое предположение маловероятным.

Для записи датированной 5 июля 139 г. (таблица Х.1), все тексты и переводы, которые я видел, датой наблюдения называют 24-й день определенного египетского месяца. Этот день соответствует 8 июля 139 г. Но если с астрономической точки зрения рассмотреть] то, как Птолемей пользуется этим наблюдением, то мы поймем, что он имел в виду египетский эквивалент дате 5 июля 139г., т. е. 21-й день месяца. В тех греческих цифрах, которыми, вероятно, пользовался Птолемей, 21 записывается как КД, а 24 как КД. Поэтому такую, ошибку сделать очень легко, и, сделал ее, возможно, сам Птолемей в оригинале «Синтаксиса».

Помещенные в последнем столбце погрешности представляют собой довольно интересный материал. Из тех семи наблюдений, которые по словам Птолемея провел он сам, во всех, кроме наблюдения 5 июля 139 г., погрешность больше 1°. Из оставшихся семи наблюдений четыре имеют незначительную погрешность, а погрешность еще в трех наблюдениях либо около, либо больше 1°.

Точки, пронумерованные на рис. Х.2 цифрами от 1 до 4 и от 11 до 14, соответствуют наблюдениям с теми же самыми номерами в таблице Х.1. Все наблюдения, кроме 13 и 14, лежат на значительном расстоянии от кривой. Наблюдение 13 принадлежит Теону, а остальные Птолемею.

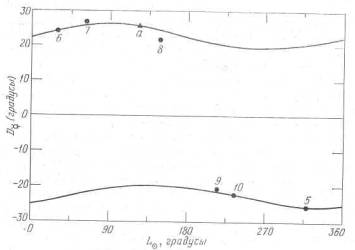
Рис Х.4. Наибольшая элонгация D_@ Меркурия как функция средней долготы Солнца L_Q на -260 г. Точками, пронумерованными от 5 до 10, показаны проведенные близко к -260 г. наблюдения, которые Птолемей использует при построении своей теории Меркурия. Точка, обозначенная буквой а и отмеченная треугольником встречается в обсуждении того, как Птолемей пользуется наблюдениями

 

Ту же самую информацию, что и на рис. Х.2, но для проведенных около -260 г. наблюдений (см. таблицу Х.1), можно получить на рис Х.4. Кривые, изображающие D_@ как функцию L_Q, вычерчены на рис Х.4 по параметрам Меркурия на -260 г. Точками, пронумерованными от 5 до 10, на рисунке отмечены наблюдения с теми же самыми номерами из таблицы Х.1. Все наблюдения, кроме наблюдения 8, лежат близко к кривой. Треугольничек, отмеченный буквой а, не наблюдение. Этой точкой на кривой мы воспользуемся при обсуждении.

Параметры і_@0 и іў_@ никак не связаны с наблюдениями Меркурия находящегося в наибольшей элонгации, но обо всех других параметрах этого не скажешь. Следовательно, по наблюдениям, внесенным в таблицу Х.1, Птолемей мог найти все параметры,   кроме  і_@0   и іў_@. Большая часть последующего обсуждения содержится в АРО в разделе XIII.8.

Начинает Птолемей с того факта, что модель для Меркурия симмет рична относительно прямой АЕ (рис. Х.З) [1]). Для наблюдения, стоящего в таблице Х.1 под номером 1, наибольшая восточная элонгация равна 21;15 градуса, а для наблюдения 2 наибольшая западная элонгация равна 21;15 градуса. Следовательно, прямая АЕ делит значения L_Q пополам. Если мы округлим значение L_Q в наблюдении 1 до 310°, то получим, что линия АЕ идет примерно от долготы 10° до долготы 190°.

Мы не можем определить значение долготы апогея а только по этим наблюдениям. Чтобы избежать многословности, необходимой при выводе этого результата, я опережу события и сразу скажу, что а равно 190° или близко к такому значению.

Птолемей подтверждает этот результат с помощью наблюдений 3 и 4. Эти наблюдения, по его словам, он также провел сам. Здесь восточная и западная элонгация были равны 26;30 градуса, так что Птолемей снова получает значение долготы апогея, близкое к 190°. Более точно, первая пара наблюдений дает значение 189;52,30 градуса, а вторая 190; 15 градуса. Разница в значениях меньше половины градуса. Птолемей решает пользоваться целым значением 190°.

Эти результаты Птолемей получает в главе IX .7 «Синтаксиса», В той же главе Птолемей обещает показать, что в древние [2]) времена долгота апогея была равна 186°, а не 190°. Сначала он приводит описание наблюдения .5, для которого L_Q=318; 10 градуса и наибольшая западная элонгация D_@=25;50. Найти же среди старых наблюдений одно наблюдение, для которого наибольшая восточная элонгация D_@=25;50, Птолемей, по его словам, не может. Поэтому он должен использовать два таких наблюдения, чтобы восточная элонгация 25;50 лежала бы между значениями элонгации для этих наблюдений. Наблюдения 6 и 7 как раз такие. Для них значения восточной элонгации равны, соответственно, 24; 10 градуса и 26;30 градуса, а значения L_Q равны 29;30 градуса и 62;50 градуса. Птолемей интерполирует по этим наблюдениям и находит соответствующее наибольшей восточной элонгации D_@=25;50 значение L_Q; L_Q=53 1/2 градуса [3]). Следовательно, на время «древних» наблюдений долгота апогея равнялась среднему арифметическому 318;10 градуса и 53;30 градуса, а это среднее равно 1855/6 градуса.

Затем Птолемей дает запись о наблюдении 8. Здесь L_Q=147;50 градуса и наибольшая восточная элонгация D_@=21;40 градуса. Старое наблюдение с наибольшей западной элонгацией D_@=21;40 Птолемей найти не может и поэтому интерполирует по наблюдениям 9 и 10. Для этих наблюдений значения L_Q равны, соответственно, 215;10 и 234;50 градуса, а наибольшая западная элонгация D_@ равна 21;00 градуса и 22;30 градуса. Интерполируя, Птолемей находит L_Q=224;10 градуса [4]). Следовательно, долгота апогея была равна среднему арифметическому 147;50 и 224;10, что точно равно 186 градусам.

Таким образом, Птолемей получил, что в эпоху Дионисия долгота апогея почти точно была равна 186°, а в его собственное время, четырьмя столетиями позже, долгота апогея почти точно равнялась- 190°. Но тогда положение апогея прецессирует на 1° в столетие. Это, как указывает Птолемей, совпадает со скоростью прецессии равноденствий, так что на фоне звезд орбита Меркурия сохраняет всегда одно и то же положение. Данный результат можно противопоставить характеру движения Солнца, чья орбита, по теории Птолемея, сохраняет одно и то же положение по отношению к точкам равноденствий [5]).

Затем Птолемей хочет найти радиус r эпицикла Меркурия. Для этого он не раз находит сумму е₁+е₂ двух эксцентриситетов (рис. Х.3). Эта сумма равна на рисунке расстоянию DE.

Обозначим через р постоянное расстояние BF (рис. Х.3). В разделе Х.1, сразу после уравнения (Х.2), я уже отмечал, что расстояние от точки Е до центра эпицикла равно Б+e₁+e₂+e₃, если среднее расстояние до апогея а равно 0°, т. е. когда в эпоху Птолемея L_Q была равна 190°. Пусть точка А - это точка, в которой находится центр эпицикла, если ±=0°; Птолемей такое положение называет апогеем. Центр эпицикла при ±=180° находится в точке G. Такое расположение соответствует L_Q=10°, но не его Птолемей называет перигеем. Если читатель набросает схему модели для ±=180°, то увидит, что расстояние от точки Е до точки G равно Б - e₁ - е₂+е₃.

Птолемею нужны были наблюдения Меркурия в наибольшей элонгации с выполнением двух условий. Одно наблюдение должно быть сделано, когда L_Q =190° (±=0°), а другое - когда L_Q =10° (a = 180°). Нужных ему «древних» наблюдений, как он говорит в главе IX.8 «Синтаксиса», нет. Объясняет Птолемей это тем, что нет достаточно ярких звезд, могущих служить точкой отсчета, которые .были бы в подобных случаях недалеко от Меркурия. Поэтому для определения положения Меркурия пришлось бы измерять большой угол между ним и яркой звездой „а это можно сделать только с помощью астролябии, которую древние [6]) наблюдатели не знали. Следовательно, он вынужден использовать свои собственные наблюдения, проведенные с помощью астролябии.

В другой работе [7]) я показал, что утверждения Птолемея просто неверны. 3 октября 134 г. звезда у Девы (а вавилонские наблюдатели часто использовали эту звезду как начало отсчета) была легко наблюдаема и находилась в нескольких градусах от Меркурия. Несомненно, такую конфигурацию можно было наблюдать много раз и раньше. 5 апреля 135 г. Меркурий находился в пределах 1° от звезды · Тельца, и если был видим Меркурий, то легко можно было увидеть и · Тельца. Эту звезду вавилоняне также часто использовали в своих наблюдениях. Кроме того, Птолемей сам говорит, что Меркурий находился в 8;20 градуса к западу от звезды ± Тельца, а это звезда первой величины. Анализ вавилонских наблюдений, проведенный в АРО, показывает, что вавилонские наблюдатели часто измеряли и большие, чем это, расстояния между небесными телами без помощи астролябии.

Таким образом, наблюдателям и без астролябии нетрудно было провести требующиеся наблюдения, несмотря на отрицание этого факта Птолемеем. Есть, конечно, какая-то вероятность, что не нашлось нужных старых наблюдений. Но, как мне кажется, истинная причина,

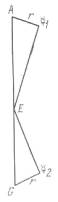
Рис. Х.5.Конфигурация птолемеевой модели для Меркурия на время мнимых наблюдений 3 октября 134 г. и 5 апреля 135 г. 3 октября 134 г. центр эпицикла Меркурия был в точке А, а сам Меркурий находился в точке @₁ 5 апреля 135 г. центр эпицикла был в точке G, а Меркурий находился в точке @₂ Как утверждает Птолемей, он измерял углы АЕ@₁ и GE@₂ и получил их соответственно равными 19;03 и 23;15 градуса. Углы в точках @₁ и @₂ прямые, поскольку в обоих случаях Меркурий был в наибольшей элонгации

 

 

почему Птолемей не использует старые наблюдения, состоит в том, что такие наблюдения не согласуются с моделью Птолемея. Поэтому он и воспользовался сфабрикованными наблюдениями, которые в этом случае он приписывает себе, а не какому-нибудь древнему наблюдателю.

В данный момент нам потребуются наблюдения, приведенные в таблице Х.1 под номерами И и 12. Соответствующие значения L_Q хотя и близки к значениям 190° и 10°, но не равны им. Однако единственная ошибка, которую мы получим, если будем считать значения L_Q точно равными 190° или 10°, происходит из-за небольшой разницы между L_Q и направлением на точку В, как это видно из точки Е (рис. Х.З). На рис. Х.5 показана конфигурация модели Птолемея для двух случаев: когда L_Q равна 190° и когда L_Q равна 10°. На этом рисунке нет никаких точек или линий, которые не потребуются нам для проведения анализа наблюдений 11 и 12.

Согласно наблюдению, проведенному по утверждению Птолемея им 3 октября 134 г., центр эпицикла был в точке А, а Меркурий находился в наибольшей западной элонгации, в точке @₁. Тогда угол в точке @₁ прямой, а угол АЕ@₁ равен 19;03 градуса. 5 апреля 135 г., опять же по Птолемею, центр эпицикла был в точке G и Меркурий находился в наибольшей восточной элонгации, в точке @₂, так что угол в точке @₂ прямой, @₂ угол GA@₂ равен 23;15 градуса.

Обозначим расстояние АЕ через R₁ а расстояние GE через R₂ Тогда из треугольников на рис. Х.5 получаем соотношения

r =R₁ sin 19;03 = 0,326 393 R₁

r =R₂ sin  23;l5 = 0,394 744 R₂

Поскольку у Птолемея не было никакого метода для определения действительных расстояний, показанных на рис. Х.5 (или Х.3), то он должен был приписать одному из расстояний произвольное значение. Птолемей приписывает значение 120 единиц расстоянию АЕ (мы обозначаем это расстояние через R₁). Тогда первое из полученных выше уравнений сразу дает нам r=39,15, т. е. r =39;09 в шестидесятеричных обозначениях. Погрешность этого вычисления незначительная. Второе уравнение дает нам теперь значение R₂.

Мы знаем, что R₁ = Б+e₁+e₂+e₃ и R₂ = Б-e₁-e₂+e₃. А так как теперь мы знаем значения R₁ и R₂, то можем найти суммы Б+e₃ и e₁+e₂. В шестидесятеричных обозначениях

Б +e₃ =109;35,

e₁+e₂ =10;25.                                                                                                            (Х.З)

Такие значения получены Птолемеем; я же получил немного другие величины. Для удобства выпишем еще раз значение r:

r =39;09.                                                                                                                   (Х.4)

Из измерений наибольшей элонгации Птолемей находит а, а', r и сумму e₁+e₂, и для этого он использует все измерения, кроме двух. А из оставшихся двух измерений ему надо найти e₃ и либо e₁ либо е₂. Зная e₁ или e₂ из уравнений (Х.З) он сможет найти все эксцентриситеты. До сих пор Птолемей пользовался симметричностью ситуации, по крайней мере, симметричностью кривой деферента. Теперь он специально использует такие обстоятельства, когда симметрии нет. Для этого он берет наблюдения, проведенные тогда, когда L_Q проходит примерно половину своего пути между точками А и G (рис. Х.5). Другими словами, Птолемею нужны два измерения наибольшей элонгации, одно восточной, другое западной, проведенные для одного и того же значения L_Q, равного либо 100°, либо 280°. Самыми подходящими наблюдениями из тех, которые он смог найти, являются наблюдение Теона (наблюдение под номером 13) и его собственное наблюдение (номер 14). Соответствующие значения L_Q немного отличаются от 100°, и это несколько усложняет дело. Сейчас мы приведем по существу птолемеево решение данной задачи, хотя сам он, конечно, излагает это решение в совершенно другой манере.

Предположим, что прямая ZBна рис. Х.6 перпендикулярна прямой AG [8]) и Меркурий находится в наибольшей восточной элонгации, т. е. в точке @₂. Поскольку по сравнению с расстоянием ZB расстояние ZE мало, то прямая ЕВ почти перпендикулярна прямой AG. Элонгация наибольшая, поэтому радиус эпицикла В@₂может повернуться на небольшой угол без изменения элонгации на заметную для наблюдателя величину. Итак, при повороте ZB на небольшой угол элонгация ВЕ@₂ не изменится. Следовательно, если угол AZBуменьшается от 90°, скажем, до 89є55', то и угол АЕ@₂ уменьшается на 5', а угол ВЕ@₂ не меняется. То же самое происходит и в случае западной элонгации, когда Меркурий находится в точке @₁.

Для наблюдения 13 значение L_Q=100;05 градуса и наибольшая восточная элонгация D_@=26;15 градуса. Следовательно, в момент наблюдения долгота Меркурия »_@ = 126;20 градуса. Если бы L_Q была точно равна 100°, а в этом случае прямая ZB была бы точно перпендикулярна прямой AG, то значение D_@ осталось бы равным 26;15 градуса (см. предыдущий абзац), так что величина »_@  получилась бы

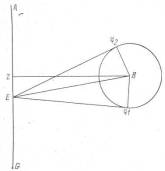
Рис. Х.6.Конфигурация эпицикла из птолемеевой модели для Меркурия на время мнимых наблюдений 4 июля 130 г. и 5 июля 139 г. Для обеих дат можно считать, что прямая ZB перпендикулярна АЕ. Мы можем предположить, что в обоих случаях центр эпицикла В был в одном и том же месте. По такому рисунку Птолемей находит расстояние ZE

 

 

 

 

 

 

 

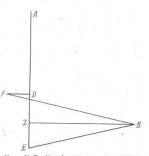Рис. Х.7. Конфигурация «кривошипа» DFи «шатуна» BF в птолемеевой модели для Меркурия на 4 июля 130 г. и на 5 июля 139 г. По рис. Х.6 Птолемей определяет расстояние ZE, а затем по этому рисунку он находит расстояния DF и BF

 

 

 

 

 

 

равной 126; 15 градуса. Аналогично, в момент наблюдения .14 L_Q= = 100;20 градуса, западная элонгация D_@=20;15 градуса и »_@=80;05 градуса. А для стоящих сейчас перед нами целей мы можем считать, что L_Q=100;00 градусам, D_@=20;15 градуса и »_@=79;45 градуса. Долгота точки А равна 190 градусам, поэтому угол АЕ@₂ равен 63;45 градуса (190-126; 15 градуса), а угол АЕ@₁ равен 110;15 градуса, если прямую ZB считать точно перпендикулярной прямой AG. Поскольку при наших условиях центр эпицикла В находится в одном и том же месте для обоих наблюдений, то угол @₁Е@₂ равен 110;15 градуса минус 63;45 градуса, т. е. угол @₁Е@₂=46;30 градуса, а оба угла BЕ@₁ и BЕ@₂ равны 23;15 градуса. Если расстояние АЕ равно 120 единицам, то радиус эпицикла, как мы знаем, равен 39;09 (равенство (Х.4)). Следовательно, можно найти [9])

EB=39;09/sin 23;15=99;9.                                                                                        (X.5)

Теперь мы хотим найти расстояние ZE, равное первому эксцентриситету e₁. Как мы помним, две элонгации на рис. Х.6 равны 26;15 и 20;15 градуса. Птолемей формулирует теорему, согласно которой угол ZBE на этом рисунке равен половине разности между двумя элонгациями, т. е. имеем точное равенство: РZBE=3 градусам. Но тогда e₁=EB sin 3°. Если взять птолемеево значение расстояния ЕВ из равенства (Х.5), то в шестидесятеричных обозначениях получим равенство е₁=5;12.

Затем Птолемей изменяет значение суммы е₁+ е₂ (уравнения (Х.3)) с 10;25 на 10;24. Мы готовы принять это изменение как допустимое. И тогда Птолемей получает, что е₁= е₂=5;12.

Для того чтобы найти из тех же самых наблюдений значение е3, воспользуемся рис. Х.7. Буквенные обозначения такие же, как и на рис. Х.3, т. е. ZE равно е₁, DZ= е₂ и DF= е₃. BF - это постоянное расстояние, которое мы обозначаем r. Прямые DF и ZB перпендикулярны прямой АЕ. Из предыдущих результатов мы знаем, что угол ZBEравен 3°, а расстояние ЕВ равно 99;9, или 99,15 в десятичных обозначениях. Следовательно, расстояние ZBравно ЕВ cos 3°=99,014 118.

Отрезок BF (=r) - это гипотенуза прямоугольного треугольника с катетами DZ (=е₂) и ZB+DF (см. рис. Х.7). Второй катет равен 99,014 118+ е₃. Таким образом, мы получили соотношение

r²= е₂²+ (99,014 118+ е₃)².

Решая одновременно это уравнение с первым из уравнений (Х.3), находим

е₃ = 5;13,

r=104;21,49.

Птолемей отмечает, что значение е₃ по существу совпадает со значениями, найденными для е₁ и е₂. Поэтому его окончательный результат такой:

е₁ = е₂ = е₃ = 5;12,

r = 104;22.                                                                                                               (Х.6)

Дойдя в главе IX.9 «Синтаксиса» до этого места, Птолемей решает вместо равенства АЕ=120 (см. рис. Х.3) ввести равенство r=60. Другими словами, он хочет изменить все расстояния в отношении 60/104;22, Если при этом мы сохраним точность до второго шестидесятеричного разряда, то получим, что каждый из эксцентриситетов равен 2;59,22, а радиус эпицикла равен 22;30,26. Птолемей округляет эти значения, соответственно, до 3 и 22;30.

Расстояние от точки Е до положения апогея кривой деферента равно сумме р и трех эксцентриситетов; при новом соглашении и с новыми значениями эта сумма равна 69. Следовательно, наибольшее расстояние до Меркурия равно 69 плюс радиус эпицикла, а это равно 91;30. Более сложные вычисления показывают, что расстояние до любой из двух точек перигея деферента равно 55;34, так что наименьшее расстояние до Меркурия равно 33;4. Это значение я и использовал в разделе IV.8 при обсуждении птолемеевой модели Вселенной.

Наконец, в главе IX. 10 «Синтаксиса» Птолемей обращается к нахождению аномалии Меркурия в некоторую эпоху и скорости изменения аномалии. Для этого он использует три наблюдения. Одно из этих наблюдений - соединение Меркурия с Луной, которое мы рассматривали в разделе Х.2 и пришли там к выводу, что наблюдение сфабриковано. Два других наблюдения приписываются Дионисию, и я вкратце приведу их описания.

1. Утром 15 ноября -264 г. Дионисий видел, что Меркурий находился на расстоянии одной луны к востоку от прямой, соединяющей звезды b Скорпиона и d Скорпиона, и он был в двух лунах к северу от b Скорпиона по широте. Под «луной» он, несомненно, подразумевает угол, равный видимому диаметру Луны. Интерпретируя наблюдение, мы можем взять этот угол равным 30'. Получившуюся конфигурацию я анализировал в АРО (с. 190-191). Меркурий находился в 46' к востоку и в 1° к северу от b Скорпиона. Момент наблюдения Дионисий не приводит. Как я вывел из его вычислений, Птолемей берет за момент наблюдения восход Солнца. Но по звездному каталогу Птолемея звезды b Скорпиона и d Скорпиона - это звезды третьей звездной величины, и, как мне кажется, моменту наблюдения скорее соответствуют 45 минут или час до восхода Солнца.

Долгота b Скорпиона по звездному каталогу Птолемея равна 216 1/3 градуса. Поскольку наблюдение было проведено почти точно за 4 столетия до эпохи каталога, то по Птолемею долгота звезды в момент наблюдения равнялась 212 1/3 градуса. Тогда долгота Меркурия была равна 212°20'+46'=213°06'. А Птоломей говорит, что долгота Меркурия равнялась 213°20'. Возможно, ошибка была допущена в процессе передачи текста, но более вероятно, как мне кажется, что Птолемей был неаккуратен при выводе долготы из наблюдения.

2. Четырьмя днями позже, утром 19 ноября -264 г., как сообщает Дионисий, Меркурий был в 1 1/2 лунах к востоку от прямой, соединяющей b Скорпиона и d Скорпиона, т. е. за четыре дня Меркурий переместился на восток на 15'. О широте ничего не говорилось.

Как ясно из рис. Х.З, существуют два значения аномалии, дающие одну и ту же долготу Меркурия. Второе наблюдение Дионисия Птолемей использует лишь для установления того факта, что во время первого наблюдения Меркурий не достиг наибольшей элонгации. А отсюда видно, какое из двух возможных значений правильное. С помощью утомительных, но очевидных вычислений по значению долготы можно получить значение номалии; подробностей я приводить не стану.

Птолемей нашел, что утром 15 ноября -264 г. аномалия была равна 212° 34'. По своему собственному наблюдению соединения Меркурия с Луной и выведенной для этого наблюдения долготе Меркурия Птолемей из вычислений получает, что во время его наблюдения 17 мая 139 г. аномалия была равна 99°27'. Изменение аномалии составило 246°53' плюс то полное число оборотов аномалии Меркурия, которое было сделано за время между двумя наблюдениями. Относительно легко увидеть, что это число равно 1268. Интервал времени составил 402 египетских года плюс 283 суток плюс 13 1/2 часа. Простым делением получаем, что изменение аномалии за сутки равно 3,106 699 градуса, или в шестидесятеричных обозначениях 3;6,24,6,58,39,51 градуса в сутки. Но в своих планетных таблицах Птолемей использует вовсе не это значение. Он берет

gў@ =3;6,24,6,59,35,50 градус/сутки.                                                                     (Х.7)

Элементарными вычислениями получаем, что в фундаментальную эпоху, т. е. в полдень по времени Александрии 26 февраля -746 г.

g@₀= 21;55 градуса.                                                 

---