ПРЕСТУПЛЕНИЕ КЛАВДИЯ ПТОЛЕМЕЯ

СОДЕРЖАНИЕ
Предисловие редактора перевода

Предисловие автора

Глава   I. Объяснение явлений в астрономии

Глава   II. Греческая математика

Глава   III. Земля

Глава   IV. Строение мира

Глава  V. Солнце и связанные с ним вопросы

Глава   VI. Долгота полной Луны

Глава   VII. Долгота Луны в любой фазе

Глава  VIII. Размеры Солнца и Луны. Расстояния до них

Глава   IX. Звезды

Глава   X. Движение Меркурия

Глава   XI. Венера и внешние планеты

Глава   XII. Некоторые второстепенные вопросы

Глава   XIII. Оценка деятельности Птолемея

Приложение А. Специальные термины и обозначения

Приложение Б. Метод Аристарха для нахождения размеров Солнца

Приложение В. Как Птолемей пользовался вавилонским календарем

Список литературы

4. Мнимые наблюдения равноденствий  и солнцестояний Птолемеем

 

Пришло время заняться теми наблюдениями равноденствий и солнцестояний, которые, по утверждению Птолемея, были проведены им самим [Птолемей, ок. 142, главы III.1 и III.7]. Три из них уже упоминались в разделе V.1; все они вошли в таблицу V.3. Сначала в таблице приводится день и час (местное время Александрии) наблюдения, как это записано у Птолемея. Затем приведено правильное время (под этим подразумевается время, вычисленное по современной теории

 

Таблица  V.3

Птолемеевы мнимые наблюдения равноденствий и солнцестояний

 

 

 

Солнца). При вычислении этого времени сначала я пользовался теорией из книги Ньюкома [1895]; в этой теории предполагается, что Солнце не имеет векового ускорения. Затем, основываясь на ранее проведенных исследованиях [АРО], я предположил, что ускорение Солнца составляет 3" в столетие за столетие. Это ускорение обусловлено приливным трением и другими негравитационными эффектами. Такая оценка справедлива, по-видимому, с точностью до 0,5" в столетие за столетие. Суммарная погрешность для вычисленных моментов времени из таблицы V.3 не превышает, вероятно, получаса. Эти моменты времени также соответствуют местному времени Александрии.

Ошибки по времени у Птолемея огромные. Моменты трех равноденствий позже почти на 28 часов, а солнцестояние получилось позже на 36 часов [1]).

Как мы видели в разделе V.2, Эвктемон, Аристарх и Гиппарх за столетия до Птолемея умели определять моменты равноденствий и солнцестояний с погрешностью в 7 часов, а это четверть погрешности Птолемея или даже меньше. Птолемей должен был определять моменты равноденствий и солнцестояний более точно. В главе III.1 «Синтаксиса», где Птолемей дает свои подозрительные наблюдения, он говорит, что проводил их с помощью приборов, описанных в начале его книги. Такие описания имеются в главе I.12 «Синтаксиса».

 

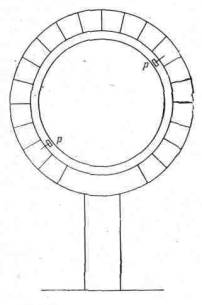 Рис. V.I. Меридианный круг Птолемея Металлическое кольцо располагается между двумя большими кругами На рисунке это кольцо разделено на интервалы в 15°, тем самым показано, что на кольце размещен градуированный круг Птолемей говорит, что у него круг был размечен в долях градуса На внутреннем кольце, которое может поворачиваться относительно внешнего, расположены две металлические пластинки РР со стрелками, указывающими а деления Вся эта конструкция устанавливается в плоскости меридиана При использовании надо поворачивать внутренний круг до тех пор, пока одна пластинка Р точно не затенит другую, и тогда стрелки показывают высоту Солнца

 

 

 

 

 

Первый прибор должен был выглядеть примерно так, как показано на рис. V.1. Два больших круга обозначают большое металлическое кольцо, установленное на подставке. Я разделил это кольцо на интервалы в 15°, показав тем самым, что оно градуировано. Птолемей говорит, что на его приборе был отмечен каждый градус и что Б каждом градусе было столько делений, сколько можно было нанести. Однако цену одного такого деления он не называет. Меньшее кольцо может поворачиваться внутри градуированного круга. На этом кольце укреплены две маленькие пластинки, отмеченные на рисунке как PP. Пластинки одинаковые, расположены на противоположных концах одного и того же диаметра и на каждой пластинке укреплена стрелка, чье показание и надо считывать с градуированного круга.

С помощью отвесов, полуденных линий и, возможно, других средств градуированный круг устанавливается в плоскости меридиана, а нулевая отметка совмещается с зенитом [2]).

Пользоваться этим прибором (по времени это можно делать только очень близко к полудню) надо так. Внутренний круг поворачивается до тех пор, пока одна пластинка Р точно не затенит другую. Таким образом получаем то, что принято называть нулевым отсчетом, и это можно сделать очень точно. Положение Солнца определяется тогда показаниями стрелок на градуированном круге [3]).

Птолемей говорит, что вторым прибором пользоваться проще и его, конечно, проще описать Прибор состоит из четверти круга, тщательно устанавливаемого в плоскости меридиана. Этот квадрант также, согласно Птолемею, разделен на градусы и части градуса, но цена деления снова не указана. В центр круга помещена маленькая булавка. Ее полуденная тень попадает на градуированный круг, и теперь можно определить положение тени. Хотя этот прибор использовать проще, он, вероятно, не дает той точности измерения, какая может быть получена при пользовании первым прибором [4]).

Если хоть один из этих приборов был сделан и использован с той тщательностью, какую подразумевает Птолемей, то точность при определении высоты Солнца должна была составлять, мне кажется, около 2'. Это значит, что точность при определении моментов равноденствий должна была быть около двух часов. Точность определения моментов солнцестояний найти труднее, но на основании раздела V.2 я полагаю ее сравнимой с точностью, достижимой при определении моментов равноденствий.

Хотя многие и пытались это сделать, но никто еще не нашел причину ошибок наблюдений, какая объясняла бы ошибки Птолемея. Никак нельзя обойти один момент: все ошибки сделаны в одном и том же направлении. Основная величина, измеряемая приборами Птолемея,- это полуденная высота Солнца. Если из-за некоторой систематической погрешности при определении высоты весеннее равноденствие получается, например, раньше чем нужно, то из-за той же самой погрешности осеннее равноденствие должно получаться позже, а на определение моментов солнцестояний эта погрешность не повлияет.

Если мы допустим, что Птолемей определял время из наблюдений (а он утверждает, что все было именно так), то мы должны допустить, что его ошибки - это случайные ошибки наблюдения. Мы будем достаточно осторожны, если при постановке простой вычислительной задачи предположим, что величина каждой погрешности наблюдения, которую можно определить по таблице V.3, достигает десяти средних квадратичных отклонений. Если мы, кроме того, предположим, что погрешности подчиняются так называемому нормальному закону распределения погрешностей, то можем найти вероятность того, что четыре последовательных измерения имеют погрешности в десять средних квадратичных отклонений каждая, причем все погрешности имеют один и тот же знак. Вероятность такого события равна одному шансу из 10⁹² [Ньютон, 1973] [5]).

Я вовсе не имею в виду, что надо рассматривать буквально эту вероятность. В каждой реальной ситуации всегда стоит вопрос о степени применимости нормального закона распределения погрешностей. В нашем случае нет достаточных оснований считать, что он применим настолько точно, чтобы количественно вероятность действительно была

равна 10^-92. Но проделанные вычисления говорят о том, что вероятность получить такие значения намного меньше вероятности, учитываемой в обычной практике. Для простоты я буду считать, что такая вероятность не могла реализоваться, и скажу, что погрешности Птолемея не могли быть случайными погрешностями наблюдения. Откуда же тогда они появились?

Ответ приходит из опыта преподавания вводного лабораторного курса по физике. В этом курсе студент получает задание поставить эксперимент или провести наблюдение, подтверждающие некоторый закон или значение важной постоянной, конечно, хорошо известное. Каждый преподаватель такого курса знает, как в этом случае поступают многие посредственные студенты. Данные, требующиеся для доказательства, они вычисляют на основе того, что надо доказать. А потом утверждают, что именно эти данные они получили из эксперимента или наблюдения.

Такой ответ подсказан словами самого Птолемея. Он подчеркивает, что его мнимые измерения, собранные в таблице V.3, подтверждают, насколько точно Гиппарх определил продолжительность года. Именно из-за того что Птолемей это подчеркивает, я и решил посмотреть, нельзя ли его данные получить вычислениями на основе тех утверждений, какие эти данные должны доказывать. Результаты соответствующих вычислений представлены в таблице V.4.

 

Таблица   V.4

Как были подделаны наблюдения Птолемея моментов равноденствий и солнцестояний

 

Проверяя продолжительность года, Птолемей в одном случае сравнивает одно свое наблюдение осеннего равноденствия с тем наблюдавшимся Гиппархом равноденствием, которое пришлось на полночь (00 часов) 27 сентября -146 г. Наблюдение Гиппарха стоит в первой строке таблицы V.4 под названием «исходное наблюдение». Птолемей утверждает [«Синтаксис», глава III.7], что осеннее равноденствие 278 годами позже было «то, которое он измерил с величайшей тщательностью» (ј№± ДЙЅ ±ЗБ№Іµ¶±Д± »·Жёµ№ГЙµ). У Гиппарха продолжительность года равнялась 365,246 666 667 суток. Если мы 278 раз прибавим эту величину к начальной эпохе и сохраним в вычислениях точность до 0,1 часа, то найдем «время, полученное из расчетов» в первой строке таблицы V.4. Это будет 25 сентября 132 г., 13,8 часа.  Птолемей  же  утверждает,  что  наблюдал  равноденствие в этот день в  14 часов.

Но продолжительность года Гиппарха Птолемей «подтверждает» не этим наблюдением. Его он использует для определения положения Солнца в фундаментальную эпоху всех своих эфемерид, 26 февраля -746 г. Продолжительность года Птолемей «проверяет» в главе III.1 «Синтаксиса». Сначала он сравнивает равноденствие, наблюдавшееся Гиппархом 27 сентября -146 г., с тем равноденствием, которое наступило 285 годами позже. В 139 г., как говорит Птолемей, «мы, несомненно, наблюдали осеннее равноденствие» (...·јµ№В µД·Б·Г±јµЅ±ГЖ±»µ¶±Д± А±»№Ѕ Д·Ѕ јµДїАЙ№Ѕ·Ѕ №Г·јµБ№±Ѕ...); он получил, что это равноденствие было в 07 часов 26 сентября 139 г. В таблице V.4 соответствующее «время, полученное из расчетов», приходится на этот день на 07,2 часа. Птолемей также «проверяет» продолжительность года, используя весеннее равноденствие -145 г., наблюдавшееся Гиппархом, и то весеннее равноденствие, которое, по его словам, он сам наблюдал в 13 часов 22 марта 140 г. (из расчетов получаем 13,2 часа).

Что же касается солнцестояний, то Птолемей не использует солнцестояние из наблюдений Гиппарха. Он использует приписываемое Метону и Эвктемону солнцестояние 27 июня -431 г. (время суток - 06 часов). Это солнцестояние Птолемей сравнивает с тем солнцестоянием, которое сам измерил «с великой тщательностью» [6])  в 02 часа 25 июня 140 г., и снова получает гиппархово значение продолжительности года [7]).

В каждом случае, если округлить до целых часов, «время, полученное из расчетов» в таблице V.4 точно совпадает с тем временем, которое, по его заверениям, Птолемей получил из наблюдений. Итак, у нас есть две гипотезы о приведенных Птолемеем наблюдениях. Гипотеза, согласно которой эти результаты действительно были получены из наблюдений, не может объяснить сами эти результаты. С другой стороны, гипотеза о том, что наблюдения являются подделкой, прямо приводит нас к таким результатам.

Вычисляя вероятность того, что моменты времени действительно были получены из наблюдений, я приравнивал погрешность в каждом из них к десяти средним квадратичным отклонениям. Это эквивалентно предположению, что среднее квадратичное отклонение каждого наблюдения около трех часов. Такое допущение разумно, но сейчас для нас неважно, верно оно или нет. Читатель может сделать любые предположения о среднем квадратичном отклонении или о других свойствах процесса измерения. Какими бы ни были эти предположения, читатель все равно не сможет объяснить погрешности в моментах времени, если будет основываться на гипотезе, что они получены из наблюдений. Причина в том, что эти значения моментов времени точно совпадают с вычисленными. Независимо от того, что явилось причиной погреш­ностей, просто невозможно получить такое совпадение для всех про­веденных, по его утверждению, наблюдений равноденствий и солнце­стояний.

Приведя первое гиппархово наблюдение весеннего равноденствия, Птолемей добавляет: «...и он утверждает, что в пятом часу в Александ­рии кольцо [8]) было одинаково освещено с обеих сторон, так что два наблюдения одного и того же равноденствия расходятся на 5 часов,...». Под «пятым часом» здесь подразумевается пятый дневной час. Если Птолемей цитирует Гиппарха правильно, то у Гиппарха это было концом пятого часа, т. е. через 11 часов после полуночи [9]). День был 24 марта -145 г.

При подделке своих собственных «наблюдений» Птолемей, как вид­но из таблицы V.4, исходит из наблюдения Гиппарха, датированного этим днем; Пшпарх провел свое наблюдение в 06 часов 24 марта -145 г. Курьезный факт, но наблюдение в Александрии, возможно, более точ­ное. По самой лучшей оценке, какую я смог сделать, весеннее равно­денствие -145 года было в 10 часов 24 марта и на Родосе, и в Алек­сандрии (их местные времена отличаются на несколько минут). У Гип­парха погрешность во времени для этого равноденствия составляет около 4 часов, а погрешность для наблюдения в Александрии была всего лишь около часа.

История опубликования вычислений, собранных в таблице V.4, довольно сложная. Проделал я их, наверное, весной 1968 г. в процессе работы над главой II своей более ранней книги [Ньютон, 1970]. Закон­чив книгу, я написал обзорную статью [Ньютон, 1969], в которую вошли и эти вычисления. Так уж случилось, что первой была опуб­ликована написанная позже статья. Почти закончив работу над кни­гой, я нашел вычисления для равноденствий (но не для солнцестояния) в докторской диссертации Бриттона [Бриттон, 1967]. Эта диссертация, насколько мне известно, до сих пор не опубликована.

В тот же самый период я изучал работы по истории древней астро­номии и обнаружил, что некоторые авторы (среди них особо следует отметить Деламбра [см. Деламбр, 1817]) подозревали подделку в дан­ных Птолемея о Солнце. Так, на с. XXVI тома 1 Деламбр пишет: «...в этом отношении [10]) никогда не возникло бы никаких сомнений, если бы равноденствия при сравнении с современными значениями не приводили бы к неприемлемой продолжительности года. Все объяс­няется, если равноденствия были вычислениями, выдаваемыми за под­линные наблюдения». Но подобные доказательства, включая и дока­зательства Деламбра, основывались на больших размерах погрешностей у Птолемея, и никто не приводил (по крайней мере в тех До­казательствах, которые я видел) весомый аргумент, содержащийся в таблице V.4. Доказательство, основанное на размерах погрешностей, может быть сведено на нет, если объяснить эти большие погрешно­сти. Но объяснение размеров ошибок не затрагивает доказательство фальсификации, основанное на совпадении «результатов наблюде­ния» с результатами вычислений (см. таблицу V.4).

Позже, когда я обратился к средневековой астрономии, я прочитал историю средневековой астрономии Деламбра [Деламбр, 1819]. К сво­ему удивлению нa c.LXVIII я нашел вычисления, проделанные Деламбром, для солнцестояния и одного равноденствия. На замечания, сделанные к его работе по древней астрономии, Деламбр отвечает во введении к своему исследованию по средневековой астрономии. По­этому я и не нашел соответствующих вычислений при изучении древней астрономии. Насколько я знаю, публикация Деламбра - первая публикация таких вычислений, и Деламбр был первым, кто дал не­опровержимое доказательство того, что Птолемей сфабриковал мо­менты подозрительных равноденствий и солнцестояний. Я не знаю, были ли подобные публикации после Деламбра, не считая, конечно, моих.

В некоторых случаях подделка информации может иметь вполне невинное объяснение [11]). Однако в обстоятельствах, преобладающих здесь, я не вижу другого объяснения, кроме умышленного обмана. Много раз подчеркивалась тщательность измерений, и измерения ис­пользовались для нахождения значений определенных астрономиче­ских параметров, которые, как говорит нам Птолемей, нужно нахо­дить из наблюдений, а вовсе не из размышлений по поводу того, каковы были намерения богов. Но отсюда еще не следует, что отвечать за этот обман должен сам Птолемей.

Возможно, у Птолемея был помощник, который работал только по указаниям Птолемея и которого Птолемей поэтому не считал заслу­живающим упоминания. Если такой помощник на самом деле сущест­вовал, то именно он мог снабжать Птолемея сфабрикованными данными вместо подлинных измерений, а Птолемей мог с полным доверием от­носиться к этим подделкам. Такая идея получает некоторое подтверж­дение в том, что Птолемей использует местоимение «мы». «Мы» проводили наблюдения равноденствий и солнцестояний. Может быть, этим «мы» Птолемей хотел подчеркнуть, что он проводил наблюдения вместе с кем-то. Однако это могло быть авторское «мы», а Птолемей использует множественное число в таких случаях, где это, без сомне­ния, авторская форма. В других случаях, например в формулировке теоремы Менелая [12]), он использует единственное число первого лица, так что он не слишком последователен в выборе между единственным числом и множественным.

В данный момент мы ничего не можем сказать об авторе показан­ных в таблице V.4 подделок. Ответ на этот вопрос требует надежного обоснования.

Ошибки у Птолемея во времени равноденствий и солнцестояния немного больше суток, поэтому погрешность птолемеевой теории Солн­ца на его собственное время несколько больше одного градуса.

 

---