ПРЕСТУПЛЕНИЕ КЛАВДИЯ ПТОЛЕМЕЯ

СОДЕРЖАНИЕ
Предисловие редактора перевода

Предисловие автора

Глава   I. Объяснение явлений в астрономии

Глава   II. Греческая математика

Глава   III. Земля

Глава   IV. Строение мира

Глава  V. Солнце и связанные с ним вопросы

Глава   VI. Долгота полной Луны

Глава   VII. Долгота Луны в любой фазе

Глава  VIII. Размеры Солнца и Луны. Расстояния до них

Глава   IX. Звезды

Глава   X. Движение Меркурия

Глава   XI. Венера и внешние планеты

Глава   XII. Некоторые второстепенные вопросы

Глава   XIII. Оценка деятельности Птолемея

Приложение А. Специальные термины и обозначения

Приложение Б. Метод Аристарха для нахождения размеров Солнца

Приложение В. Как Птолемей пользовался вавилонским календарем

Список литературы

9. Узел лунной орбиты

 

До сих пор мы рассматривали движение Луны только в плоскости ее орбиты, причем только в полнолуние. Теперь можно было бы рас­смотреть движение Луны в ее орбитальной плоскости в других фазах. Но я последую за Птолемеем и займусь движением самой орбитальной плоскости.

Общую картину мы описали в разделе I.4. Плоскость движения Луны образует с плоскостью эклиптики угол немного больше 5°. Угол этот, называемый наклоном орбиты, не постоянен. Его среднее значение равно 5,144°. Наклон орбиты колеблется с периодом 9,3 го­да около этого среднего значения с отклонениями в каждую сторону примерно на 0,15°. Кроме того, наклон орбиты подвержен и другим изменениям.

Прямая пересечения плоскости движения Луны с плоскостью эк­липтики называется линией узлов. Луна пересекает эту линию два раза в месяц. Если Луна пересекает линию узлов, переходя с южной стороны эклиптики на северную, то направление с Земли на Луну на­зывается восходящим узлом. Если же Луна попадает на эту линию, переходя с северной на южную сторону эклиптики, то направление на Луну называется нисходящим узлом. В плоскости эклиптики линия узлов движется на запад. Полный обход эклиптики занимает примерно 18,6 года. Желательно было бы уметь определять, скажем, восходя­щий узел в любой момент времени. В этом разделе я покажу, как это делали греческие астрономы. А тот способ, каким греческие астрономы определяли наклон орбиты, я, следуя Птолемею, рассмотрю позднее (в других разделах).

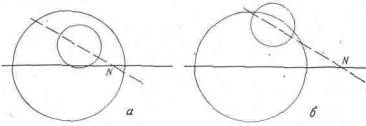Рис. VI.3. Луна и тень Земли во время лунных затмений. На обеих частях рисунка горизонтальная линия обозначает эклиптику, наклонная штриховая линия - это линия движения Луны, большой круг - это тень Земли, маленький круг - Луна. Точка N - это узел лунной орбиты. Угол между линией движения Луны и эклипти­кой увеличен. На рис. VI.3, а Луна проходит настолько близко к центру тени, что она полностью затемнена. На рис. VI.3, б Луна проходит мимо центра тени на большем расстоянии и затемнена только частично

 

Птолемей говорит, что в изучении движения узлов он будет поль­зоваться методом и некоторыми данными, которыми до него пользо­вался Гиппарх [главы IV.2 и IV.9 «.Синтаксиса»]. На самом же деле этот метод был известен еще Аристарху, жившему за 1 1/2 столетия до Гиппарха и за 4 1/2 столетия до Птолемея. В этом методе снова исполь­зуются лунные затмения. Соответствующая геометрия показана на рис. VI.3.

Во время движения Солнца вокруг Земли Земля всегда отбрасы­вает в пространстве тень в противоположном от Солнца направлении. Ось этой тени, очевидно, лежит в плоскости эклиптики. Представим теперь, что во время полнолуния на том же самом расстоянии, на ка­ком находится Луна, поставили экран. На экране мы увидели бы по­перечное сечение тени, и это поперечное сечение, так же как диски Солнца и Луны, имело бы свой видимый диаметр. Размеры тени зави­сят от расстояния до Земли. В каждой данной точке размер тени за­висит и от расстояния от Земли до Солнца, но влияние этого расстоя­ния мало, и, насколько я могу судить по рассуждениям Птолемея, он его не учитывал.

Горизонтальная прямая на обеих частях рис. VI.3   представляет плоскость эклиптики,  а  большой  круг - это  контур  земной тени.

В среднем видимый радиус тени немного больше 41' [1]). Видимый радиус диска Луны в среднем 15'33". Сумма двух радиусов в среднем боль­ше 56'.

Ясно, что никакая часть Луны не будет закрыта тенью, если толь­ко расстояние от центра Луны до центра тени не меньше суммы радиу­сов. Для простоты рассуждений я буду считать, что эта сумма равна 1°. Конечно, в каждом отдельном случае надо использовать соответст­вующее этому случаю значение. Для большинства полнолуний Луна находится в нескольких градусах от центра тени и затмения не проис­ходит. В среднем у нас бывает около 1,54 лунных затмений в год [2]), т. е. примерно 1 затмение на каждые 8 полнолуний. В полнолуние затмение будет только тогда, когда Луна подойдет ближе, чем на 1° к центру тени.

На обеих частях рис. VI.3 наклонная штриховая прямая обозна­чает линию движения центра Луны. В действительности угол между этой линией и эклиптикой (это наклон орбиты) немного больше 5°. На рисунке угол увеличен. Если узел N находится недалеко от центра тени (рис. VI.За), то Луна проходит настолько близко к центру тени, что затмение будет полным. Если узел дальше от центра тени (рис. VI.3б), то только часть Луны попадает в тень Земли. В этом случае затмение будет частичным.

Пусть затмение не полное. Тогда наибольшая фаза затмения гово­рит нам о том, какая часть диаметра Луны попадает в тень Земли в момент середины затмения [3]). Из рисунка ясно, что наибольшая фаза затмения зависит от расстояния между Луной и узлом в момент сере­дины затмения. Зависит величина затмения и от видимых размеров как тени Земли, так и Луны. Я уже говорил, что это в свою очередь зависит от расстояния от Земли до Луны. В меньшей степени видимые размеры тени зависят от расстояния от Земли до Солнца.

На обеих частях рис. VI.3 Луна находится к северу от эклиптики и движется влево (на восток) от восходящего узла. Имеются три других возможных конфигурации. Луна может быть к югу от эклиптики и двигаться к восходящему узлу, может быть севернее эклиптики и двигаться к нисходящему узлу и может быть южнее эклиптики и двигаться от нисходящего узла. Если Луна во время частичного зат­мения находится к северу от эклиптики, то она затемнена с южной сто­роны.

В своих рассуждениях Птолемей использует угол в плоскости орбиты Луны от восходящего узла до положения средней Луны. Мы эту величину назовем И, средний аргумент широты [4]). Ясно, что зная И и среднюю долготу L(, мы можем определить положение узла.

Сперва нам хотелось бы найти  И2, величину изменения И за сутки. Гиппарх искал такие два затмения, которые имели бы одинаковые наибольшие фазы и во время которых Луна находилась бы по одну и ту же сторону от эклиптики и около одного и того же узла; кроме того, требовалось, чтобы Луна во время этих затмений находилась бы на одинаковом расстоянии от Земли [«Синтаксис», глава IV.2] [5]). По таким двум затмениям Гиппарх находит, что средний аргумент ши­роты совершает 5 923 полных оборота за 5 458 месяцев. А поскольку продолжительность месяца известна, то получается

И2 =13;13,45,39,40,17,19= 13,229 350 330 8   градус/сутки.     (VI.13)

Для проверки найденного значения Птолемей использует два затмения. Первое затмение наблюдалось в Вавилоне 25 апреля -490 г. Середина затмения пришлась на середину шестого ночного часа. Лу­на была затемнена на 2/12 своего диаметра с южной стороны. Следо­вательно, Луна была к северу от эклиптики. Луна находилась около нисходящего узла. Птолемей заключает, что от его фундаментальной эпохи [6])  до середины этого затмения прошло 256 лет плюс 122 суток плюс 10 1/4 часа среднего времени.

Второе затмение наблюдалось в Александрии 5 апреля 125 г. Се­редина затмения пришлась на 3 3/5 часа до полуночи [7]). Луна также была затемнена на 2/12 своего диаметра с южной стороны и находи­лась около нисходящего узла. Птолемей получает, что середина затме­ния была через 871 год плюс 256 суток плюс 8 1/12 часа среднего вре­мени после фундаментальной эпохи. Таким образом, между затмения­ми прошло 615 лет плюс 133 суток плюс 21 5/6 часа.

Обстоятельства затмений аналогичны. Следовательно, действитель­ная Луна сделала целое число обращений относительно узла за про­межуток между затмениями. Но этого нельзя сказать о средней Луне. В первое затмение вычисленное значение аномалии равно 100;19 гра­дуса, а е_С=-5,0 градуса. Поэтому средней Луне не хватает до пол­ного числа обращений 9;53 градуса. Однако если мы воспользуемся равенством (VI.13), то найдем, что величине И до полного числа обо­ротов не хватает 10;2 градуса. Поэтому равенство (VI.13) надо так подправить, чтобы суммарное изменение на интервале между затме­ниями получилось бы равным 0;9. Изменить И2 надо на 0;0,0,0,8,39,18 градуса в сутки. Тогда получаем

И2 = 13;13,45,39,48,56,37= 13,229 350 998 7 градус/сутки   (VI.14)

Все арифметические вычисления я проверил.

Заметим, что у Птолемея была только одна значащая цифра (0;9 градуса, или 9') в той величине, которую надо прибавить к значе­нию, найденному Гиппархом. А Птолемей прибавляет число с пятью значащими цифрами.

Теперь Птолемею надо определить И₀, значение И в фундаменталь­ную эпоху. Для этого, как он говорит, ему требуются два затмения с одной и той же наибольшей фазой. Кроме того, Луна в моменты этих затмений должна находиться по одну и ту же сторону эклиптики и на одном и том же расстоянии от Земли, но около разных узлов [8]). В качестве первого затмения Птолемей берет затмение 8 марта-719 г. Он уже использовал это затмение для нахождения радиуса эпицикла. Луна была затемнена на одну четверть своего диаметра с южной сто­роны и находилась около восходящего узла. В качестве второго зат­мения он берет одно из тех затмений, которые использовал Гиппарх. Это затмение наблюдалось в Вавилоне 19 ноября -501 г. через 6 1/3 часа после захода Солнца. Луна была затемнена на одну четверть сво­его диаметра с южной стороны, но находилась около нисходящего узла. Птолемей получает, что затмение в Александрии было через 10 1/4 часа среднего времени после полудня. Между затмениями прошло 218 египетских лет плюс 309 суток плюс 23 1/2 часа среднего времени.

Если воспользоваться равенством (VI.14), мы получим, что средний аргумент широты И совершил 17 610 полных оборотов и повернулся еще на 160;4 градуса [9]). По значению аномалии мы можем сказать, что дей­ствительная Луна во время первого затмения была на 59' позади сред­ней Луны, а во время второго затмения - на 13' позади средней Лу­ны. Следовательно, действительная Луна сделала вокруг узла 17 610 обращений плюс 160;50 градуса. Пусть во время первого затмения она была, скажем, на Xградусов перед восходящим узлом, а во время вто­рого - на такую же величину позади нисходящего узла. Тогда Х==1/2 (180-160;50)=9;35 градуса.

Во время первого затмения действительная Луна была в 9;35 гра­дуса впереди восходящего узла и на 0;59 градуса позади средней Лу­ны. Следовательно, средняя Луна была на 10;34 градуса выше восходя­щего узла. То есть И =10;34 во время первого затмения. Теперь нахо­дим, что в фундаментальную эпоху

И₀=84;15 градуса.       (VI.15)

Отметим, что Птолемей измеряет И не от восходящего узла, как это делают современные астрономы, а от положения средней Луны, соответствующего наибольшей широте. Отсюда Птолемей получает зна­чение 354;15 для величины, которую он называет движением средней Луны по широте.

Исследуем подлинность использованных затмений. С этой целью составлена таблица VI.5. В нее включены четыре только что обсуждав­шихся затмения в порядке их появления в тексте «Синтаксиса». Сна­чала мы приводим момент середины затмения (время среднее) [10]), дан­ный Птолемеем и вычисленный по его таблицам. Затем приведены три значения наибольшей фазы затмения. Первое значение - то, которое дает Птолемей в описании затмения, второе - значение, которое я вычислил по птолемеевым таблицам затмений [11]). Третье значение полу­чено по современной теории затмений.

Таблица   VI.5

Время и наибольшая фаза четырех лунных затмений

Наибольшие фазы даны в принятых единицах. Одна единица в данном контексте - дробь 1/12. Так, например, если величина зат­мения задана как 3 единицы, то это значит, что была затемнена 1/4 (=3/12) часть диаметра.

Для первых двух затмений время, вычисленное по таблицам Пто­лемея, расходится с тем временем, которое приводит Птолемей, на 16 минут. Так что вряд ли эти затмения сфабрикованы. Однако наи­большие фазы затмений свидетельствуют об обратном. Для каждого из этих затмений наибольшая фаза, вычисленная по таблицам, равна 1,8 единицы. Округлив это значение до 2 единиц, получаем наиболь­шую фазу, приводимую Птолемеем. А ведь эти затмения имели далеко не одинаковую величину. Как показывает последняя колонка, раз­ница составляла 0,7 единицы. А использовать эти затмения так, как это делает Птолемей, можно только в том случае, если их наибольшие фазы одинаковые. Из таблиц затмений Птолемея или из элементарной геометрии мы получаем, что изменение наибольшей фазы затмения на одну единицу соответствует изменению примерно на 30' аргумента широты. Если наибольшие фазы затмений различаются на 0,7 единицы, то разница между значениями аргумента широты будет около 21', а Птолемей брал эту разность равной нулю. Птолемей использует затмения, чтобы получить   поправку в 9' к результатам Гиппарха. По­грешность же измерений составляла 21', так что здесь одна видимость поправки, и каждый компетентный астроном должен это осознавать.

Прежде чем перейти к двум другим затмениям в таблице VI.5, исследуем, с какой точностью можно определить наибольшую фазу лунного затмения невооруженным глазом. Ранее [Ньютон, 1970, с. 215] я изучал измерения наибольшей фазы для трех затмений, сделанных китайскими астрономами, и двенадцати затмений, наблюдавшихся мусульманскими астрономами. Все наблюдения были проведены меж­ду 21 января 585 г. и 12 апреля 990г. Все измерения наибольшей фазы затмения сделаны невооруженным глазом. Среднее квадратичное от­клонение измерения наибольшей фазы затмения оказалось равным 0,98 единицы. Для простоты я округлил это значение до 1 условной единицы наибольшей фазы затмения. Тогда при сравнении наиболь­ших фаз двух затмений (Птолемей проводит такое сравнение для зат­мений 25 апреля -490 г. и 5 апреля 125 г.) среднее квадратичное от­клонение разности равно 1,4 единицы, что соответствует 42' в положе­нии узла. Любая поправка, меньшая этого значения, с теми данными, какие были у Птолемея, бессмысленна, если только эта поправка не получалась из анализа многих пар затмений [12]).

Теперь обратимся к затмениям 8 марта -719 г. и 19 ноября -501 г. Птолемей использует эти затмения для нахождения И₀, среднего ар­гумента широты в фундаментальную эпоху. Затмение 8 марта -719 г. Птолемей уже использовал при вычислении эксцентриситета Луны, и мы знаем, что это затмение сфабриковано [13]). Нет никаких очевидных причин, почему Птолемей должен был предпочесть одно значение И₀ другому, и поэтому непонятно, зачем он пользуется поддельными дан­ными для нахождения И₀. Затмение 8 марта -719 г., несомненно, сфаб­риковано, но совсем для других целей, и, возможно, Птолемею было просто удобно использовать его и в этом случае. Значение И₀ зависит и от второго затмения, поэтому непонятно, зачем его подделывать. Тем не менее измеренное время этого затмения согласуется с таблица­ми Птолемея с точностью до 1 минуты. Такое совпадение возможно, но подозрительно. Мы должны допустить, что затмение могло быть сфабриковано, пусть и по непонятной нам причине.

Не все ясно и с наибольшими фазами этих затмений. Для того чтобы Птолемей мог использовать их так, как он это делает, они долж­ны были иметь одинаковую наибольшую фазу. И Птолемей сообщает, что величина обоих затмений была равна 3 единицам. Если эти затме­ния - подделка, то скорее всего их величины вычислены по табли­цам Птолемея. Но по таблицам мы получили бы 2,4 единицы. Я не могу придумать никакую правдоподобную вычислительную процедуру которая приводила бы к значению 3 единицы. Кроме того, последний столбец показывает, что правильные значения были 1,5 и 2,2 еди­ницы.

Возможно, у Птолемея были подлинные описания затмений, но для своих подделок он изменяет в них время. Его интересовало только совпадение наибольших фаз затмений, а не количественное выражение этих наибольших фаз, так что у него не было необходимости менять наибольшие фазы затмений в подлинных описаниях. Может быть, наибольшие фазы затмений были даны как 3 единицы, а Птолемей не стал их менять. Тогда погрешность в размерах наибольшей фазы для затмения 8 марта -719 г. составит 1,5 единицы. Это много, но все же возможно. В данном астрономами стран ислама описании затмения 22 июня 856 г. имеется такая ошибка [Ньютон, 1970, с. 215].

Что же получено в этом разделе? Мы уже знаем, что затмение 8 марта -719 г.- подделка, по крайней мере это относится ко времени затмения. Анализ, проведенный в этом разделе, не позволяет с абсо­лютной уверенностью говорить ни о том, что все остальные затмения в таблице VI.5 подлинные, ни о том, что они поддельные. Какие-то данные в этих описаниях могут быть подлинными, какие-то сфабрико­ванными. В приложении. В мы приводим некоторые факты, относящие­ся ко всем затмениям, которые Птолемей датирует по вавилонскому календарю. На основании материала Приложения В можно предполо­жить, что записи 19 ноября -501 г. и 25 апреля -490 г. поддельные. Но других подтверждений такому выводу нет. Поэтому эти затмения и затмение 5 апреля 125 г. мы относим к категории «могут быть подлин­ными». По всей видимости, использовать любые данные из этих запи­сей в астрономических исследованиях не стоит.

 

---